2025年经纶学典学霸黑白题高中数学必修第一册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年经纶学典学霸黑白题高中数学必修第一册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第120页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
8. $\boldsymbol{★★★}$(2025·江苏南京高一月考)若函数$ f(x) = 2\sin \left(\omega x + \frac{\pi}{3}\right)(\omega > 0) $在区间$[0, \pi]$上恰有两个最大值,则实数$\omega$的取值范围是_。
答案:
8.$\left[\frac{13}{6},\frac{25}{6}\right)$ 解析:因为$\omega>0$,$x\in[0,\pi]$,所以$\omega x+\frac{\pi}{3}\in\left[\frac{\pi}{3},\omega\pi+\frac{\pi}{3}\right]$.又$f(x)=2\sin\left(\omega x+\frac{\pi}{3}\right)(\omega>0)$在区间$[0,\pi]$上恰有两个最大值,所以$\omega\pi+\frac{\pi}{3}\in\left[\frac{5\pi}{2},\frac{9\pi}{2}\right)$,解得$\omega\in\left[\frac{13}{6},\frac{25}{6}\right)$.故答案为$\left[\frac{13}{6},\frac{25}{6}\right)$.
9. $\boldsymbol{★★}$(2025·陕西榆林高一期末)函数$ f(x) = A\sin(\omega x + \varphi)(A > 0, \omega > 0, 0 < \varphi < \pi) $在一个周期内的图象如图所示。
(1)求$ f(x) $的解析式;
(2)将$ f(x) $的图象向左平移$\frac{\pi}{3}$个单位长度后得到函数$ g(x) $的图象,设$ h(x) = f(x) + g(x) $,证明:$ h(x) $为奇函数。
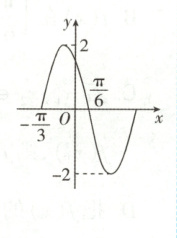
(1)求$ f(x) $的解析式;
(2)将$ f(x) $的图象向左平移$\frac{\pi}{3}$个单位长度后得到函数$ g(x) $的图象,设$ h(x) = f(x) + g(x) $,证明:$ h(x) $为奇函数。

答案:
9.
(1)解:由题图得$A=2$,$\frac{T}{2}=\frac{\pi}{6}-\left(-\frac{\pi}{3}\right)=\frac{\pi}{2}$,则$T=\frac{2\pi}{\omega}=\pi$,即$\omega=2$,此时$f(x)=2\sin(2x+\varphi)$.因为$-\frac{\pi}{3}+\frac{\pi}{6}=-\frac{\pi}{12}$,则该函数图象一个最高点为$\left(-\frac{\pi}{12},2\right)$,代入点$\left(-\frac{\pi}{12},2\right)$得$\sin\left(-\frac{\pi}{6}+\varphi\right)=1$,则$-\frac{\pi}{6}+\varphi=\frac{\pi}{2}+2k\pi(k\in\mathbf{Z})$,即$\varphi=\frac{2\pi}{3}+2k\pi(k\in\mathbf{Z})$.又因为$0<\varphi<\pi$,所以$k=0$,$\varphi=\frac{2\pi}{3}$,故$f(x)=2\sin\left(2x+\frac{2\pi}{3}\right)$.
(2)证明:由题意得$g(x)=2\sin\left[2\left(x+\frac{\pi}{3}\right)+\frac{2\pi}{3}\right]=-2\sin\left(2x+\frac{\pi}{3}\right)$,则$h(x)=2\sin\left(2x+\frac{2\pi}{3}\right)-2\sin\left(2x+\frac{\pi}{3}\right)$.
因为$h(-x)=2\sin\left(-2x+\frac{2\pi}{3}\right)-2\sin\left(-2x+\frac{\pi}{3}\right)=2\sin\left[-\left(2x+\frac{\pi}{3}\right)+\pi\right]-2\sin\left[-\left(2x+\frac{2\pi}{3}\right)+\pi\right]=2\sin\left(2x+\frac{\pi}{3}\right)-2\sin\left(2x+\frac{2\pi}{3}\right)=-h(x)$,且其定义域为$\mathbf{R}$,关于原点对称,所以$h(x)$为奇函数.
(1)解:由题图得$A=2$,$\frac{T}{2}=\frac{\pi}{6}-\left(-\frac{\pi}{3}\right)=\frac{\pi}{2}$,则$T=\frac{2\pi}{\omega}=\pi$,即$\omega=2$,此时$f(x)=2\sin(2x+\varphi)$.因为$-\frac{\pi}{3}+\frac{\pi}{6}=-\frac{\pi}{12}$,则该函数图象一个最高点为$\left(-\frac{\pi}{12},2\right)$,代入点$\left(-\frac{\pi}{12},2\right)$得$\sin\left(-\frac{\pi}{6}+\varphi\right)=1$,则$-\frac{\pi}{6}+\varphi=\frac{\pi}{2}+2k\pi(k\in\mathbf{Z})$,即$\varphi=\frac{2\pi}{3}+2k\pi(k\in\mathbf{Z})$.又因为$0<\varphi<\pi$,所以$k=0$,$\varphi=\frac{2\pi}{3}$,故$f(x)=2\sin\left(2x+\frac{2\pi}{3}\right)$.
(2)证明:由题意得$g(x)=2\sin\left[2\left(x+\frac{\pi}{3}\right)+\frac{2\pi}{3}\right]=-2\sin\left(2x+\frac{\pi}{3}\right)$,则$h(x)=2\sin\left(2x+\frac{2\pi}{3}\right)-2\sin\left(2x+\frac{\pi}{3}\right)$.
因为$h(-x)=2\sin\left(-2x+\frac{2\pi}{3}\right)-2\sin\left(-2x+\frac{\pi}{3}\right)=2\sin\left[-\left(2x+\frac{\pi}{3}\right)+\pi\right]-2\sin\left[-\left(2x+\frac{2\pi}{3}\right)+\pi\right]=2\sin\left(2x+\frac{\pi}{3}\right)-2\sin\left(2x+\frac{2\pi}{3}\right)=-h(x)$,且其定义域为$\mathbf{R}$,关于原点对称,所以$h(x)$为奇函数.
10. $\boldsymbol{★★}$(2025·江苏镇江高一期末)给出以下三个条件:①函数$ y = f(x) $图象的两条相邻对称轴之间的距离为$\frac{\pi}{2}$;②$ f\left(-\frac{\pi}{6}\right) = 0 $;③对任意的$ x \in \mathbf{R} $,$ f(x) \leq f\left(\frac{\pi}{12}\right) $。请从这三个条件中任选一个将下面的题目补充完整,并解答该题。
已知函数$ f(x) = \sin \left(\omega x + \frac{\pi}{3}\right)(0 < \omega < 3) $,且满足_。
(1)求$\omega$的值;并用“五点法”作出函数$ y = f(x) $在一个周期内的图象;
(2)将函数$ f(x) $的图象向右平移$\frac{\pi}{3}$个单位长度后,再将此时图象上各点的纵坐标不变,横坐标变为原来的2倍,得到函数$ y = g(x) $的图象,若$ y = g(x) $的图象与直线$ y = k $在区间$[0, \pi]$上有且只有一个交点,求实数$ k $的取值范围。
已知函数$ f(x) = \sin \left(\omega x + \frac{\pi}{3}\right)(0 < \omega < 3) $,且满足_。
(1)求$\omega$的值;并用“五点法”作出函数$ y = f(x) $在一个周期内的图象;
(2)将函数$ f(x) $的图象向右平移$\frac{\pi}{3}$个单位长度后,再将此时图象上各点的纵坐标不变,横坐标变为原来的2倍,得到函数$ y = g(x) $的图象,若$ y = g(x) $的图象与直线$ y = k $在区间$[0, \pi]$上有且只有一个交点,求实数$ k $的取值范围。
答案:
10.解:①(或②或③)
(1)若选择①,可知两条相邻对称轴之间的距离为半个周期,即$\frac{T}{2}=\frac{\pi}{\omega}=\frac{\pi}{2}$,可得$\omega=2$;
若选择②,由$f\left(-\frac{\pi}{6}\right)=0$可得$f\left(-\frac{\pi}{6}\right)=\sin\left(-\frac{\pi}{6}\omega+\frac{\pi}{3}\right)=0$,因此$-\frac{\pi}{6}\omega+\frac{\pi}{3}=k\pi,k\in\mathbf{Z}$,解得$\omega=2-6k,k\in\mathbf{Z}$.又$0<\omega<3$,所以$\omega=2$;
若选择③,由对任意的$x\in\mathbf{R},f(x)\leqslant f\left(\frac{\pi}{12}\right)$可得$f\left(\frac{\pi}{12}\right)$取得最大值,即$f\left(\frac{\pi}{12}\right)=\sin\left(\frac{\pi}{12}\omega+\frac{\pi}{3}\right)=1$,即$\frac{\pi}{12}\omega+\frac{\pi}{3}=\frac{\pi}{2}+2k\pi,k\in\mathbf{Z}$,解得$\omega=2+24k,k\in\mathbf{Z}$.又$0<\omega<3$,可得$\omega=2$.
因此$f(x)=\sin\left(2x+\frac{\pi}{3}\right)$,列表取值如下:
$2x+\frac{\pi}{3}$:$0$,$\frac{\pi}{2}$,$\pi$,$\frac{3\pi}{2}$,$2\pi$
$x$:$-\frac{\pi}{6}$,$\frac{\pi}{12}$,$\frac{\pi}{3}$,$\frac{7\pi}{12}$,$\frac{5\pi}{6}$
$f(x)$:$0$,$1$,$0$,$-1$,$0$
描点连线得到图象,如图①,

(2)将函数$f(x)$的图象向右平移$\frac{\pi}{3}$个单位长度可得$y=\sin\left[2\left(x-\frac{\pi}{3}\right)+\frac{\pi}{3}\right]=\sin\left(2x-\frac{\pi}{3}\right)$的图象,再将图象上各点的纵坐标不变,横坐标变为原来的2倍,可得$g(x)=\sin\left(2×\frac{1}{2}x-\frac{\pi}{3}\right)=\sin\left(x-\frac{\pi}{3}\right)$的图象,当$x\in[0,\pi]$时,$x-\frac{\pi}{3}\in\left[-\frac{\pi}{3},\frac{2\pi}{3}\right]$,所以$g(x)=\sin\left(x-\frac{\pi}{3}\right)\in\left[-\frac{\sqrt{3}}{2},1\right]$,画出$g(x)=\sin\left(x-\frac{\pi}{3}\right)$在$[0,\pi]$上的图象,如图②,

若$y=g(x)$的图象与直线$y=k$在区间$[0,\pi]$上有且只有一个交点,由图②可得当$k\in\left[-\frac{\sqrt{3}}{2},\frac{\sqrt{3}}{2}\right)\cup\{1\}$时,满足题意,因此实数$k$的取值范围为$\{1\}\cup\left[-\frac{\sqrt{3}}{2},\frac{\sqrt{3}}{2}\right)$.
10.解:①(或②或③)
(1)若选择①,可知两条相邻对称轴之间的距离为半个周期,即$\frac{T}{2}=\frac{\pi}{\omega}=\frac{\pi}{2}$,可得$\omega=2$;
若选择②,由$f\left(-\frac{\pi}{6}\right)=0$可得$f\left(-\frac{\pi}{6}\right)=\sin\left(-\frac{\pi}{6}\omega+\frac{\pi}{3}\right)=0$,因此$-\frac{\pi}{6}\omega+\frac{\pi}{3}=k\pi,k\in\mathbf{Z}$,解得$\omega=2-6k,k\in\mathbf{Z}$.又$0<\omega<3$,所以$\omega=2$;
若选择③,由对任意的$x\in\mathbf{R},f(x)\leqslant f\left(\frac{\pi}{12}\right)$可得$f\left(\frac{\pi}{12}\right)$取得最大值,即$f\left(\frac{\pi}{12}\right)=\sin\left(\frac{\pi}{12}\omega+\frac{\pi}{3}\right)=1$,即$\frac{\pi}{12}\omega+\frac{\pi}{3}=\frac{\pi}{2}+2k\pi,k\in\mathbf{Z}$,解得$\omega=2+24k,k\in\mathbf{Z}$.又$0<\omega<3$,可得$\omega=2$.
因此$f(x)=\sin\left(2x+\frac{\pi}{3}\right)$,列表取值如下:
$2x+\frac{\pi}{3}$:$0$,$\frac{\pi}{2}$,$\pi$,$\frac{3\pi}{2}$,$2\pi$
$x$:$-\frac{\pi}{6}$,$\frac{\pi}{12}$,$\frac{\pi}{3}$,$\frac{7\pi}{12}$,$\frac{5\pi}{6}$
$f(x)$:$0$,$1$,$0$,$-1$,$0$
描点连线得到图象,如图①,

(2)将函数$f(x)$的图象向右平移$\frac{\pi}{3}$个单位长度可得$y=\sin\left[2\left(x-\frac{\pi}{3}\right)+\frac{\pi}{3}\right]=\sin\left(2x-\frac{\pi}{3}\right)$的图象,再将图象上各点的纵坐标不变,横坐标变为原来的2倍,可得$g(x)=\sin\left(2×\frac{1}{2}x-\frac{\pi}{3}\right)=\sin\left(x-\frac{\pi}{3}\right)$的图象,当$x\in[0,\pi]$时,$x-\frac{\pi}{3}\in\left[-\frac{\pi}{3},\frac{2\pi}{3}\right]$,所以$g(x)=\sin\left(x-\frac{\pi}{3}\right)\in\left[-\frac{\sqrt{3}}{2},1\right]$,画出$g(x)=\sin\left(x-\frac{\pi}{3}\right)$在$[0,\pi]$上的图象,如图②,

若$y=g(x)$的图象与直线$y=k$在区间$[0,\pi]$上有且只有一个交点,由图②可得当$k\in\left[-\frac{\sqrt{3}}{2},\frac{\sqrt{3}}{2}\right)\cup\{1\}$时,满足题意,因此实数$k$的取值范围为$\{1\}\cup\left[-\frac{\sqrt{3}}{2},\frac{\sqrt{3}}{2}\right)$.
$\boldsymbol{★★★}$ 已知函数$ f(x) = \sin(\omega x + \varphi) $($ \omega > 0 $)在$\left[-\frac{\pi}{3}, \frac{\pi}{6}\right]$上单调,且$ f\left(\frac{\pi}{6}\right) = f\left(\frac{4\pi}{3}\right) = -f\left(-\frac{\pi}{3}\right) $,则$\omega$的取值不可能为 (
A.$\frac{3}{5}$
B.$\frac{7}{5}$
C.$\frac{9}{5}$
D.$\frac{12}{7}$
B
)A.$\frac{3}{5}$
B.$\frac{7}{5}$
C.$\frac{9}{5}$
D.$\frac{12}{7}$
答案:
B 解析:由$f(x)$在$\left[-\frac{\pi}{3},\frac{\pi}{6}\right]$上单调,$f\left(\frac{\pi}{6}\right)=-f\left(-\frac{\pi}{3}\right)$,故$\frac{T}{2}\geqslant\frac{\pi}{6}-\left(-\frac{\pi}{3}\right)=\frac{\pi}{2}\Rightarrow T\geqslant\pi$,而$\frac{\pi}{2}-\left(-\frac{\pi}{2}\right)=\pi$,则$\frac{\pi}{2}\omega+\varphi=0$,又$f\left(\frac{\pi}{6}\right)=f\left(\frac{4\pi}{3}\right)$,依次讨论$x=\frac{4\pi}{3}$对应为点$C,A,D,E$四种情况,
若$\frac{4\pi}{3}-\left(-\frac{\pi}{3}\right)=\frac{T}{2}\omega=\frac{5\pi}{3}\omega$,则$\omega=\frac{3}{5}$,满足$T\geqslant\pi$;若$\frac{4\pi}{3}-\frac{\pi}{6}=\frac{7\pi}{6}=T$,则$\omega=\frac{12}{7}$,满足$T\geqslant\pi$;由$\frac{3\pi}{4}-\frac{\pi}{6}=\frac{7\pi}{12}=\frac{T}{2}=\frac{\pi}{\omega}$,则$\omega=\frac{12}{7}$,若$\frac{3\pi}{4}-\left(-\frac{\pi}{12}\right)=\frac{3\pi}{4}-\left(-\frac{\pi}{12}\right)=\frac{5\pi}{6}=\frac{T}{2}=\frac{\pi}{\omega}$,则$\omega=\frac{6}{5}$,满足$T\geqslant\pi$;若$\frac{4\pi}{3}-\frac{\pi}{6}=2T=\frac{7\pi}{6}=\frac{2\pi}{\omega}$,则$\omega=\frac{24}{7}$,不满足$T\geqslant\pi$,其他情况均不符合.综上,B不可能,A,C,D可能.故选B.
若$\frac{4\pi}{3}-\left(-\frac{\pi}{3}\right)=\frac{T}{2}\omega=\frac{5\pi}{3}\omega$,则$\omega=\frac{3}{5}$,满足$T\geqslant\pi$;若$\frac{4\pi}{3}-\frac{\pi}{6}=\frac{7\pi}{6}=T$,则$\omega=\frac{12}{7}$,满足$T\geqslant\pi$;由$\frac{3\pi}{4}-\frac{\pi}{6}=\frac{7\pi}{12}=\frac{T}{2}=\frac{\pi}{\omega}$,则$\omega=\frac{12}{7}$,若$\frac{3\pi}{4}-\left(-\frac{\pi}{12}\right)=\frac{3\pi}{4}-\left(-\frac{\pi}{12}\right)=\frac{5\pi}{6}=\frac{T}{2}=\frac{\pi}{\omega}$,则$\omega=\frac{6}{5}$,满足$T\geqslant\pi$;若$\frac{4\pi}{3}-\frac{\pi}{6}=2T=\frac{7\pi}{6}=\frac{2\pi}{\omega}$,则$\omega=\frac{24}{7}$,不满足$T\geqslant\pi$,其他情况均不符合.综上,B不可能,A,C,D可能.故选B.
查看更多完整答案,请扫码查看


