《2025年经纶学典学霸黑白题高中数学必修第一册苏教版》

13. 证明下列各题。
(1) 已知$x,y,z$都是正数，求证：$(x + y)(y + z)(z + x)\geq 8xyz$。
(2) 已知$a,b$都是正实数，当$a + b = 1$时，求证：$(1+\frac{1}{a})(1+\frac{1}{b})\geq 9$。

答案： 13.证明：
(1)$\because x＞0,y＞0,z＞0,\therefore x + y\geq2\sqrt{xy}＞0,y + z\geq2\sqrt{yz}＞0$，$x + z\geq2\sqrt{xz}＞0$，当且仅当$x = y = z$时，等号成立，$\therefore(x + y)(y + z)(x + z)\geq8\sqrt{xy}\sqrt{yz}\sqrt{xz}=8xyz,\therefore(x + y)(y + z)(x + z)\geq8xyz$.
(2)$\because a,b$都是正实数，且$a + b = 1,\therefore(1+\frac{1}{a})(1+\frac{1}{b})=(1+\frac{a + b}{a})(1+\frac{a + b}{b})=(2+\frac{b}{a})(2+\frac{a}{b})=5 + 2(\frac{b}{a}+\frac{a}{b})\geq5 + 4\sqrt{\frac{b}{a}·\frac{a}{b}}=9$，当且仅当$a = b=\frac{1}{2}$时，等号成立.

14. * (2025·江西南昌高一月考)某单位采用新工艺将二氧化碳转化为化工产品，其月处理成本$y$(元)与月处理量$x$(吨)的函数关系式为$y = 2x^{2}-180x + 20000$。则当月处理量为100吨时，可以使每吨的平均处理成本最低。 (A)

A.100
B.150
C.200
D.250

答案： 14.A 解析：依题意，每吨的平均处理成本为$\frac{y}{x}=2(x+\frac{10000}{x}) - 180\geq2·2\sqrt{x·\frac{10000}{x}} - 180 = 220$，当且仅当$x=\frac{10000}{x}$，即$x = 100$时取等号，所以当月处理量为100吨时，可以使每吨的平均处理成本最低.故选A.

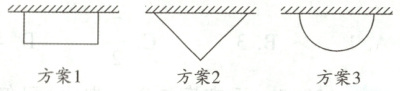
15. 某班计划在劳动实践基地内种植蔬菜，班长买回来8米长的围栏，准备围成一边靠墙(墙足够长)的菜园，为了让菜园面积尽可能大，同学们提出了围成矩形、直角三角形、半圆这三种方案，最佳方案是 (C)


A.方案1
B.方案2
C.方案3
D.方案1或方案2

答案：
15.C 解析：方案1：如图①，设$AD = x$米，则$AB = (8 - 2x)$米，则菜园面积$S = x(8 - 2x)= - 2x^2 + 8x = - 2(x - 2)^2 + 8$，当$x = 2$时，此时菜园最大面积为8平方米；

方案2：如图②，依题意$AB + AC = 8$米，所以$S_{\triangle ABC}=\frac{1}{2}AB· AC\leq\frac{1}{2}·\frac{(AB + AC)^2}{4}=8$平方米，当且仅当$AB = AC = 4$米时取等号.

方案3：半圆的半径$=\frac{8}{\pi}$米，所以此时菜园最大面积$=\pi×(\frac{8}{\pi})^2÷2=\frac{32}{\pi}$平方米$＞8$平方米.故选C.

16. (2025·河北唐山高一月考)阿基米德有句名言：“给我一个支点，我就能撬起整个地球！”这句话说的便是杠杆原理，即“动力×动力臂 = 阻力×阻力臂”。现有一商店使用两臂不等长的天平称黄金，一位顾客到店里预购买20 g黄金，售货员先将10 g的砝码放在天平左盘中，取出$x$ g黄金放在天平右盘中使天平平衡；再将10 g的砝码放在天平右盘中，取$y$ g黄金放在天平左盘中使天平平衡，最后将称得的$x$ g和$y$ g黄金交给顾客，则顾客购得的黄金质量大于20 g(填“大于”“小于”或“等于”)

答案： 16.大于 解析：设天平左臂长为$x_1$，右臂长为$x_2$，且$x_1\neq x_2$，$\begin{cases}10x_1 = xx_2\\yx_1 = 10x_2\end{cases}$解得$\begin{cases}x = \frac{10x_1}{x_2}\\y = \frac{10x_2}{x_1}\end{cases}\because x_2\neq x_1,\therefore x + y = \frac{10x_1}{x_2}+\frac{10x_2}{x_1}＞2\sqrt{\frac{10x_2}{x_1}·\frac{10x_1}{x_2}} = 20$.故答案为大于.

17. * (2025·广东惠州高一月考)已知$x ＞ 0,y ＞ 0$，且$2x + y = 1$，则$\frac{2}{x}+\frac{1}{y}$的最小值为 (B)

A.6
B.9
C.12
D.18

答案： 17.B 解析：因为$x＞0,y＞0$，且$2x + y = 1$，所以$\frac{2}{x}+\frac{1}{y}=(2x + y)(\frac{2}{x}+\frac{1}{y}) = 5+\frac{2x}{y}+\frac{2y}{x}\geq5 + 2\sqrt{\frac{2x}{y}·\frac{2y}{x}} = 9$，当且仅当$\begin{cases}\frac{2x}{y}=\frac{2y}{x}\\2x + y = 1\\x＞0\\y＞0\end{cases}$即当$x = y=\frac{1}{3}$时，等号成立，故$\frac{2}{x}+\frac{1}{y}$的最小值为9.故选B.

18. * (2025·江苏淮安高一期中)已知正数$a,b$满足$3a + b = ab$，则$a + 3b$的最小值是 (A)

A.16
B.$6\sqrt{3}$
C.$2\sqrt{2}$
D.18

答案： 18.A 解析：已知$a＞0,b＞0$满足$3a + b = ab$，得$\frac{1}{a}+\frac{3}{b}=1$，则$a + 3b=(a + 3b)(\frac{1}{a}+\frac{3}{b})+10\geq2\sqrt{\frac{3b}{a}·\frac{3a}{b}}+10 = 16$，当且仅当$\frac{3b}{a}=\frac{3a}{b}$，即$a = b = 4$时等号成立.故选A.

19. * (2025·河北石家庄高一月考)若$a,b ＞ 0$，且$a^{2}+b^{2}=ab + 3$，则$ab$的最大值为3。

答案： 19.3 解析：因为$a^2 + b^2=ab + 3$，所以$ab + 3=a^2 + b^2\geq2ab,ab\leq3$，当且仅当$a = b=\sqrt{3}$时，等号成立，所以$ab$的最大值为3.故答案为3.

20. * 已知$x,y$均为正数，且$\frac{1}{x}+\frac{9}{y}=2$，则$x + y$的最小值为8。

答案： 20.8 解析：因为$x,y$均为正数，且$\frac{1}{x}+\frac{9}{y}=2$，所以$x + y=(x + y)(\frac{1}{x}+\frac{9}{y})\frac{1}{2}=10+\frac{y}{x}+\frac{9x}{y}\geq10 + 2\sqrt{\frac{y}{x}·\frac{9x}{y}}=8$，当且仅当$\frac{y}{x}=\frac{9x}{y}$，即$y = 3x = 6$时取等号，所以$x + y$的最小值为8.故答案为8.

21. * (2025·湖南衡阳高一月考)对于任意$0 ＜ x ＜ 4$，$m ＞ \frac{x}{x^{2}+1}$恒成立，则 (D)

A.$m ＞ \frac{2}{5}$
B.$m ＞ \frac{3}{5}$
C.$m ＞ \frac{3}{10}$
D.$m ＞ \frac{1}{2}$

答案： 21.D 解析：对于任意$0＜x＜4$，$m＞\frac{x}{x^2 + 1}$恒成立，则$m＞(\frac{x}{x^2 + 1})_{\max}$，而$\frac{x}{x^2 + 1}\leq\frac{1}{x+\frac{1}{x}}\leq\frac{1}{2\sqrt{x·\frac{1}{x}}}=\frac{1}{2}$，当且仅当$x = 1$时取等号，所以$m＞\frac{1}{2}$.故选D.

22. * (2025·福建福州高一期中)当$x ＞ 0,y ＞ 0$时，$\frac{1}{x}+\frac{4}{y}\geq\frac{m}{x + y}$，则实数$m$的最大值为 (A)

A.9
B.8
C.4
D.1

答案： 22.A 解析：因为当$x＞0,y＞0$时，$\frac{1}{x}+\frac{4}{y}\geq\frac{m}{x + y}$，所以$(x + y)·(\frac{1}{x}+\frac{4}{y})\geq m$.又因为$(x + y)(\frac{1}{x}+\frac{4}{y})=\frac{y}{x}+\frac{4x}{y}+5\geq2\sqrt{\frac{y}{x}·\frac{4x}{y}}+5 = 9$，当且仅当$\frac{y}{x}=\frac{4x}{y}$，即$y = 2x$时，等号成立，所以$m\leq9$，所以实数$m$的最大值为9.故选A.