第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
1. (2023·岳阳)观察下列式子:$1^{2}-1 = 1×0$;$2^{2}-2 = 2×1$;$3^{2}-3 = 3×2$;$4^{2}-4 = 4×3$;$5^{2}-5 = 5×4\cdots\cdots$
依此规律,则第$n$($n$为正整数)个等式是
依此规律,则第$n$($n$为正整数)个等式是
$n^{2}-n=n(n - 1)$
。
答案:
$n^{2}-n=n(n - 1)$
2. (2024·云南改编)有一组按一定规律排列的代数式:$2x$,$3x^{2}$,$4x^{3}$,$5x^{4}$,$6x^{5}$,$\cdots$,则第$n$个代数式是
(n + 1)x^{n}
。
答案:
$(n + 1)x^{n}$
3. 符号“$f$”“$g$”分别表示一种运算,它们对一些数的运算结果如下:
(1)$f(1)=0$,$f(2)=1$,$f(3)=2$,$f(4)=3$,$\cdots$,$f(10)=9\cdots\cdots$
(2)$g(\frac{1}{2}) = 2$,$g(\frac{1}{3}) = 3$,$g(\frac{1}{4}) = 4$,$g(\frac{1}{5}) = 5$,$\cdots$,$g(\frac{1}{11}) = 11\cdots\cdots$
利用以上规律计算:$g(\frac{1}{2025}) - f(2025) =$
(1)$f(1)=0$,$f(2)=1$,$f(3)=2$,$f(4)=3$,$\cdots$,$f(10)=9\cdots\cdots$
(2)$g(\frac{1}{2}) = 2$,$g(\frac{1}{3}) = 3$,$g(\frac{1}{4}) = 4$,$g(\frac{1}{5}) = 5$,$\cdots$,$g(\frac{1}{11}) = 11\cdots\cdots$
利用以上规律计算:$g(\frac{1}{2025}) - f(2025) =$
1
。
答案:
1
4. 观察这组数:$\frac{2}{3}$,$\frac{6}{9}$,$\frac{12}{27}$,$\frac{20}{81}$,$\frac{30}{243}$,$\cdots$,它们是按一定规律排列的,那么这组数的第$n$个数是
$\frac{n(n + 1)}{3^{n}}$
。
答案:
$\frac{n(n + 1)}{3^{n}}$
5. 湖南师大附中校本经典题
如图,我们做一个游戏:从大拇指开始,按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→食指…的顺序依次数正整数$1$,$2$,$3$,$4$,$5\cdots$。当第$n$次数到中指时,恰好数到的数是
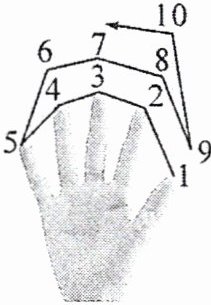
如图,我们做一个游戏:从大拇指开始,按照大拇指→食指→中指→无名指→小指→无名指→中指→食指→大拇指→食指…的顺序依次数正整数$1$,$2$,$3$,$4$,$5\cdots$。当第$n$次数到中指时,恰好数到的数是
4n - 1
(用含$n$的代数式表示)。
答案:
$4n - 1$
6. (2023·重庆)用长度相同的木棍按如图所示的规律拼图案,其中第①个图案用了$9$根木棍,第②个图案用了$14$根木棍,第③个图案用了$19$根木棍,第④个图案用了$24$根木棍……按此规律排列下去,则第⑧个图案用的木棍根数是(

A.$39$
B.$44$
C.$49$
D.$54$
B
)
A.$39$
B.$44$
C.$49$
D.$54$
答案:
B
7. (2024·安康汉滨区期末)如图,每个图案均是由长度相等的火柴棒按一定的规律拼接而成的。第$1$个图案需要$8$根火柴棒;第$2$个图案需要$14$根火柴棒;第$3$个图案需要$20$根火柴棒……依此规律拼下去。
(1)第$4$个图案需要火柴棒
(2)第几个图案中需要$602$根火柴棒?
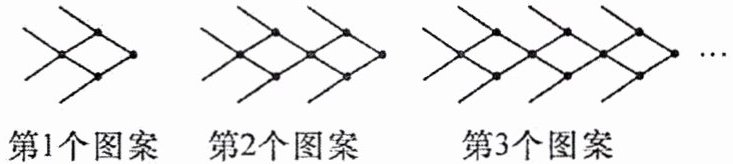
(1)第$4$个图案需要火柴棒
26
根,第$n$个图案需要火柴棒(6n + 2)
根(用含$n$的式子表示)。(2)第几个图案中需要$602$根火柴棒?

答案:
(1)26 (6n + 2)
(2)由题意,得$6n + 2 = 602$,解得$n = 100$.
∴第100个图案需要602根火柴棒.
(1)26 (6n + 2)
(2)由题意,得$6n + 2 = 602$,解得$n = 100$.
∴第100个图案需要602根火柴棒.
8. 新考向 推理能力 下列数阵是由$50$个偶数按照$5×10$排成的,框内有四个数。
(1)猜测:图中框内四个数之和与数字$4$有什么关系?
(2)在数阵中任意画一个类似于(1)中的框,设左上角的数为$x$,那么怎样表示其他三个数?
(3)任意移动这个框,是否都能得到(1)中的结论?你能说明理由吗?
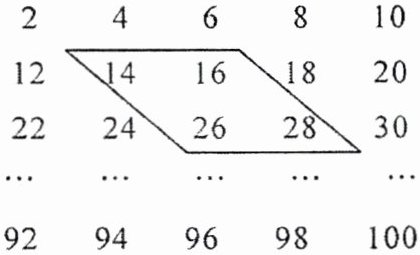
(1)猜测:图中框内四个数之和与数字$4$有什么关系?
(2)在数阵中任意画一个类似于(1)中的框,设左上角的数为$x$,那么怎样表示其他三个数?
(3)任意移动这个框,是否都能得到(1)中的结论?你能说明理由吗?

答案:
(1)图中框内四个数之和能被4整除.
(2)其他三个数分别为$x + 2$,$x + 12$,$x + 14$.
(3)能.理由如下:$x + x + 2 + x + 12 + x + 14 = 4x + 28 = 4(x + 7)$.
∵$x$为整数,
∴$x + 7$为整数.
∴任意移动这个框,框内四个数之和都能被4整除.
(1)图中框内四个数之和能被4整除.
(2)其他三个数分别为$x + 2$,$x + 12$,$x + 14$.
(3)能.理由如下:$x + x + 2 + x + 12 + x + 14 = 4x + 28 = 4(x + 7)$.
∵$x$为整数,
∴$x + 7$为整数.
∴任意移动这个框,框内四个数之和都能被4整除.
查看更多完整答案,请扫码查看


