《2025年名校课堂七年级数学上册人教版陕西专版》

1. (1)加法交换律：$a + b =$b+a.
例：$3 + (-5) =$（-5）$+ 3$.
(2)加法结合律：$(a + b) + c =$a+(b+c).
例：$[(-3) + (-31)] + (+31) = (-3) + [$（-31）$+$（+31）$]$.

答案： 1.
(1)b+a（-5）
(2)a+(b+c)（-31） (+31）

2. 小磊解题时，将式子$(-\frac{1}{6}) + (-7) + \frac{5}{6} + (-4)$先变成$[(-\frac{1}{6}) + \frac{5}{6}] + [(-7) + (-4)]$再计算结果，则小磊运用了(B)

A.加法交换律
B.加法交换律和加法结合律
C.加法结合律
D.无法判断

答案： 2.B

3. 下列变形中，运用运算律正确的是(D)

A.$2 + (-1) = 1 + 2$
B.$3 + (-2) + 5 = (-2 + 5) - 3$
C.$[6 + (-3)] + 5 = [6 + (-5)] + 3$
D.$\frac{1}{3} + (-2) + (+\frac{2}{3}) = (\frac{1}{3} + \frac{2}{3}) + (-2)$

答案： 3.D

4. 计算$43 + (-77) + 27 + (-43)$的结果是(C)

A.50
B.$-104$
C.$-50$
D.104

答案： 4.C

5. 若$a$，$b$互为相反数，则$(-2025) + a + 2024 + b =$-1.

答案： 5.-1

6. 运用加法的运算律计算下列各题：
(1)$(-2\frac{1}{3}) + \frac{1}{4} + (-\frac{1}{4})$.
(2)$18 + (-12) + (-9) + 12$.
(3)$(-6.5) + (-1.4) + (-7.6) + 5.5$.
(4)$(-\frac{1}{3}) + 13 + (-\frac{2}{3}) + 17$.

答案： 6.解：
(1)原式$=(-2\frac{1}{3})+[\frac{1}{4}+(-\frac{1}{4})]=(-2\frac{1}{3})+0=-2\frac{1}{3}。$
(2)原式=[18+(-9)]+[(-12)+12]=9+0=9。
(3)原式=[(-6.5)+5.5]+[(-1.4)+(-7.6)]=(-1)+(-9)=-10。
(4)原式$=[(-\frac{1}{3})+(-\frac{2}{3})]+(13+17)=-1+30=29。$

7. 一架直升机从海拔$1000$米的高原上起飞，第一次上升了$1500$米，第二次上升了$-1200$米，此时这架直升机的海拔是1300米.

答案： 7.1300

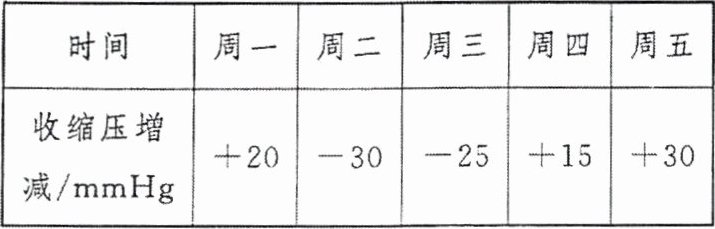
8. 某病人每天下午需要测量血压，该病人上周日收缩压为$120mmHg$.下表是该病人这周每天与前一天相比收缩压的变化情况，则该病人本周五的收缩压是130$mmHg$.

答案： 8.130

9. (教材P35习题T8变式)某公司2025年前四个月盈亏的情况如下(记盈余为正)：$-160.5$万元、$-120$万元、$+65.5$万元、$+280$万元.求2025年前四个月该公司总的盈亏情况.

答案： 9.解：(-160.5)+(-120)+(+65.5)+(+280)=[(-160.5)+(+65.5)]+[(-120)+(+280)]=(-95)+160=65(万元)。答：2025年前四个月该公司共盈余65万元。