《2025年名校课堂七年级数学上册人教版陕西专版》

12. 湖南师大附中校本经典题 若单项式 $x^{a + 2}y^{2}$ 与 $3xy^{b}$ 的和是单项式，则 $a^{b}$ 的值是 (D)

A.$-2$
B.$2$
C.$-1$
D.$1$

答案： 12.D

13. 已知多项式 $x^{2}+3kxy-y^{2}-9xy + 10$ 中不含 $xy$ 项，则 $k=$3.

答案： 13.3

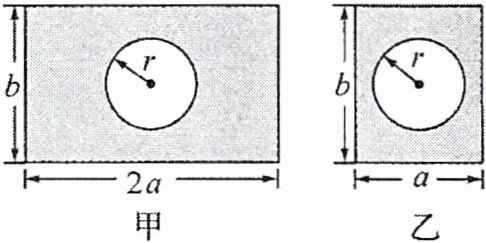
14. 兰生复旦校本经典题 如图，在甲、乙两面墙壁上各挖去一个半径相同的圆形空洞，用来安装窗花，其余部分涂满油漆，则根据图中所标尺寸，两面墙上的油漆面积一共为3ab−2πr².

答案： $14.3ab−2πr^{2}$

15. 先合并同类项，再求值：
(1) $\frac{1}{4}a^{2}b-0.4ab^{2}-\frac{1}{2}a^{2}b+\frac{2}{5}ab^{2}-1$，其中 $a = 2$，$b=-1$.
(2) $3(x - y)^{2}-3(x - y)-2(x - y)^{2}+3(x - y)-2(x - y)+7$，其中 $x - y = 3$.

答案： 15.解：
(1)原式$=(\frac {1}{4}a^{2}b−\frac {1}{2}a^{2}b)+(−0.4ab^{2}+\frac {2}{5}ab^{2})−1=−\frac {1}{4}a^{2}b−1.$当a = 2,b=−1时，原式$=−\frac {1}{4}×2^{2}×(−1)−1=0. (2)$原式$=(x−y)^{2}−2(x−y)+7.$当x−y=3时，原式$=3^{2}−2×3 + 7=10.$

16. 新考向 真实情境 某学校组织七、八年级全体同学参观七亘大捷爱国主义教育基地(位于平定县东回镇七亘村).七年级租用 $45$ 座大巴车 $x$ 辆，$55$ 座大巴车 $y$ 辆；八年级租用 $30$ 座中巴车 $y$ 辆，$55$ 座大巴车 $x$ 辆.假设每辆车恰好坐满学生.
(1)七、八年级各有多少名学生?
(2)七、八年级共有多少名学生?
(3)当 $x = 4$，$y = 6$ 时，该学校七、八年级共有多少名学生?
]

答案： 16.解：
(1)七年级有(45x + 55y)名学生，八年级有(55x + 30y)名学生.
(2)45x + 55y + 55x + 30y=(100x + 85y)名.答：七、八年级共有(100x + 85y)名学生.
(3)当x = 4,y = 6时，100x + 85y=100×4 + 85×6=910.答：当x = 4,y = 6时，该学校七、八年级共有910名学生.

17. 北京四中校本经典题 有这样一道题：
当 $a = 2024$，$b=-2025$ 时，求多项式 $7a^{3}-6a^{3}b+3a^{2}b+3a^{3}+6a^{3}b-3a^{2}b-10a^{3}+2026$ 的值.
小明说：“本题中‘$a = 2024$，$b=-2025$’是多余的条件.”小强马上反对说：“这不可能，多项式中含有 $a$ 和 $b$，不给出 $a$，$b$ 的值，怎么能求出多项式的值呢?”
你同意哪名同学的观点? 请说明理由.

答案： 17.解：同意小明的观点.理由：原式$=(7a^{3}+3a^{3}−10a^{3})+(−6a^{3}b + 6a^{3}b)+(−3a^{2}b + 3a^{2}b)+2026=2026.$
∴该多项式的值与a,b的取值无关.
∴同意小明的观点.

18. 多项式 $m-3m + 5m-7m+\cdots-99m$ 合并同类项的结果为 (B)

A.$-100m$
B.$-50m$
C.$-200m$
D.$-150m$

答案： 18.B