《2025年名校课堂七年级数学上册人教版陕西专版》

11. (2024·西安交大附中期末)元朝朱世杰所著的《算学启蒙》中,记载了这样一道题:“良马日行二百四十里,驽马日行一百六十里,驽马先行一十二日,问良马几何日追及之?”其大意是:快马每天行 240 里,慢马每天行 160 里,慢马先行 12 天,快马几天可追上慢马? 设快马 x 天可追上慢马,由题意可列方程为 (D)

A.$\frac {x}{240}=\frac {x+12}{160}$
B.$\frac {x}{240}=\frac {x}{160}-12$
C.$240(x-12)=160x$
D.$240x=160(x+12)$

答案： D

12. (2024·陕西副卷)塞罕坝机械林场经过三代务林人的接续奋斗,已知现在该林场的林木总蓄积比原来增加了 1 007 万立方米,已成为目前世界上最大的人工林场;又知现在该林场的林木总蓄积比原来的 31 倍还多 17 万立方米,请问该林场原来的林木总蓄积是多少万立方米?

答案： 12.解：设该林场原来的林木总蓄积是x万立方米，则现在该林场的林木总蓄积是(31x+17)万立方米.根据题意，得31x+17-x=1007，解得x=33.答：该林场原来的林木总蓄积是33万立方米.

13. (2024·商洛期末)某商场正在热销两种苹果,精品苹果每千克定价 20 元,普通苹果每千克定价 5 元,店庆期间商场决定开展促销活动,活动方案如下:
现某公司为回馈员工,要到该商场购买精品苹果 200 千克,普通苹果 x 千克$(x＞100$,且只能选择一种方案购买).
(1)用含 x 的代数式分别表示该公司选择方案一和方案二购买时所需的钱数.(结果化成最简形式)
(2)若该公司选择方案一和方案二购买时付款相同,求该公司购买了多少千克普通苹果.

答案： 13.解：
(1)方案一需付款：200×20+5(x-100)=(5x+3500)元.方案二需付款：(200×20+5x)×90%=(4.5x+3600)元.
(2)由题意，得5x+3500=4.5x+3600，解得x=200.答：该公司购买了200千克普通苹果.

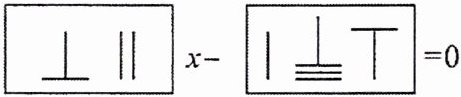
14. 新考向 数学文化 算筹是我国古代的计算方法之一,纵式表示一到五时,竖放的每一根代表一,表示六到九时,横放一根代表五,其余算筹竖放在下面,横式则相反. 在表示多位数时,个位用纵式,十位用横式,百位用纵式,千位用横式,以此类推,遇零则置空.如图所示的两个框内的算筹所表示的两位数、三位数分别为方程的一次项系数及常数项,则推算 x 表示的数为3.

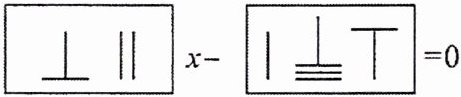
答案： 3

15. (2024·西安高新一中期末)我们规定:若关于 x 的一元一次方程$a+x=b(a≠0)$的解为$x=\frac {b}{a}$,则称该方程为“商解方程”. 例如:$2+x=4$的解为$x=2$,且$2=\frac {4}{2}$,则方程$2+x=4$是“商解方程”. 请回答下列问题:
(1)判断$3+x=4.5$是不是“商解方程”.
(2)若关于 x 的一元一次方程$4+x=2(m-3)$是“商解方程”,求 m 的值.

答案： 15.解：
(1)是.理由如下：
∵3+x=4.5的解为x=1.5，且$1.5=\frac{4.5}{3}，$
∴方程3+x=4.5是“商解方程”.
(2)由“商解方程”的定义，得$x=\frac{m-3}{2}.$解关于x的一元一次方程4+x=2(m-3)，得x=2m-10，
∴$\frac{m-3}{2}=2m-10，$解得$m=\frac{17}{3}.$