《2025年名校课堂七年级数学上册人教版陕西专版》

12. 下列说法中，正确的是(D)

A.任何数都有倒数
B.同号两数相乘，符号不变
C.互为相反数的两数相乘，积一定为负
D.两个有理数的积的绝对值，等于这两个有理数的绝对值的积

答案： D

13. 如果$a + b＞0$，且$ab＞0$，那么(A)

A.$a＞0$，$b＞0$
B.$a$，$b$异号，且正数的绝对值较小
C.$a＜0$，$b＜0$
D.$a$，$b$异号，且负数的绝对值较小

答案： A

14. (2024·西安高陵区期中)若有理数$a$，$b$互为倒数，$c$，$d$互为相反数，则$c + d+\frac{1}{ab}=$1.

答案： 1

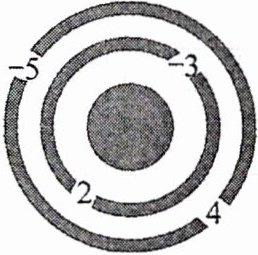
15. 新考向 真实情境 一座两道环路的数字迷宫如图所示，外环两个路口的数字分别为-5，4，内环两个路口的数字分别为-3，2.要想进入迷宫中心需破解密码：内外环两个路口的数相乘，若乘积最大，沿这两个路口就可到达迷宫中心，则乘积最大的值是15.

答案： 15

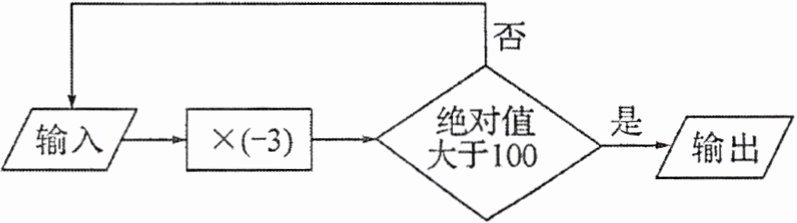
16. 按如图所示的程序计算，如果输入的数是2，那么输出的数是162.

答案： 162

17. 计算：
(1)$(-0.8)×(-\frac{7}{4})$.
(2)$1\frac{3}{5}×(-3\frac{3}{4})$.

答案：
(1)原式=$\frac{4}{5}×\frac{7}{4}=\frac{7}{5}$.
(2)原式=$\frac{8}{5}×(-\frac{15}{4})=-(\frac{8}{5}×\frac{15}{4})=-6$.

18. 华师二附中校本经典题 下列说法是否正确.如果认为正确，请说明理由；如果认为错误，请举例说明.
(1)两个正数中，较大数的倒数反而小.
(2)两个有理数中，较大数的倒数反而小.

答案： 解：
(1)正确，理由如下：对于一个正数a，其倒数可写作$\frac{1}{a}$，那么两个正数中，较大数的倒数的分母比较小数的倒数的分母大，所以较大数的倒数反而小.
(2)不正确.例如：两个有理数-1和1，其中-1为较小数，1为较大数，它们的倒数分别为-1,1.因为-1＜1，所以此时较大数的倒数比较小数的倒数.故该说法不正确.

19. 已知$\vert x\vert = 3$，$\vert y\vert = 7$.
(1)若$xy＜0$，求$x - y$的值.
(2)若$x - y＜0$，求$xy$的值.

答案： 解：
(1)
∵|x| = 3，
∴x = ±3.
∵|y| = 7，
∴y = ±7.
∵xy＜0，
∴x,y异号.
∴x = 3,y = -7或x = -3,y = 7.当x = 3,y = -7时，x - y = 3 - (-7) = 10；当x = -3,y = 7时，x - y = -3 - 7 = -10.
∴x - y的值是±10.
(2)
∵x = ±3,y = ±7，且x - y＜0，
∴x = 3,y = 7或x = -3,y = 7.
∴xy的值是±21.