《2025年优佳学案（云南）九年级物理全一册人教版》

5. 图甲是用某款$3D$打印笔进行立体绘画时的场景,打印笔通电后,笔内电阻丝发热使笔内绘画材料熔化。加热电路简化后如图乙所示,电源电压恒为$6\space V$,$R_{1}和R_{2}$为发热电阻丝,只闭合$S_{1}$时低温挡工作,$S_{1}$、$S_{2}$都闭合时高温挡工作,高温挡和低温挡的功率比为$4:3$,$R_{1}= 4\space \Omega$。忽略电阻丝电阻随温度的变化,求：

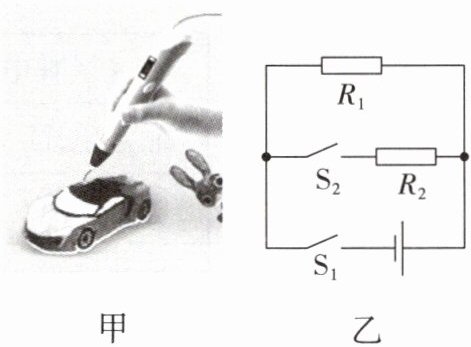
(1)低温挡工作时,通过$R_{1}$的电流。
(2)低温挡的功率。
(3)$R_{2}$的电阻。

答案：
(1)只闭合S₁时为低温挡，电路中只有R₁接入，通过R₁的电流$I = \frac{U}{R_{1}}=\frac{6V}{4\Omega}=1.5A$。
(2)低温挡功率$P_{低}=UI = 6V×1.5A = 9W$。
(3)高温挡与低温挡功率比为4:3，故高温挡功率$P_{高}=\frac{4}{3}P_{低}=\frac{4}{3}×9W = 12W$。S₁、S₂都闭合时，R₁与R₂并联，总功率$P_{高}=P_{1}+P_{2}$，其中$P_{1}=P_{低}=9W$，则$P_{2}=P_{高}-P_{1}=12W - 9W = 3W$。由$P=\frac{U^{2}}{R}$得$R_{2}=\frac{U^{2}}{P_{2}}=\frac{(6V)^{2}}{3W}=12\Omega$。
(1)1.5A
(2)9W
(3)12Ω

6. 某饮水机有加热挡和保温挡,其电路原理如图所示,其额定电压为 $220\space V$,$R_{1}$、$R_{2}$为定值电阻,$R_{1}= 110\space \Omega$,保温挡的额定功率为 $44\space W$。

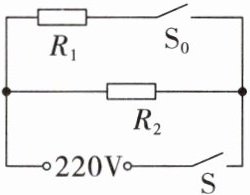
(1)求保温挡正常工作时电路中的电流。
(2)求加热时饮水机的额定功率。
(3)饮水机将水加热至沸腾用时$3\space min$,共消耗电能$0.02\space kW·h$,求此时饮水机的实际电压。

答案：
(1) 保温挡正常工作时，根据 $ P = UI $ 可得电流 $ I = \frac{P}{U} = \frac{44\space W}{220\space V} = 0.2\space A $。
(2) 保温挡总电阻 $ R_{保} = \frac{U^2}{P_{保}} = \frac{(220\space V)^2}{44\space W} = 1100\space \Omega $，此时电路为 $ R_2 $ 单独工作，故 $ R_2 = 1100\space \Omega $。加热挡时 $ R_1 $ 与 $ R_2 $ 并联，总电阻 $ R_{并} = \frac{R_1R_2}{R_1+R_2} = \frac{110\space \Omega × 1100\space \Omega}{110\space \Omega + 1100\space \Omega} = 100\space \Omega $，加热功率 $ P_{加} = \frac{U^2}{R_{并}} = \frac{(220\space V)^2}{100\space \Omega} = 484\space W $。
(3) 消耗电能 $ W = 0.02\space kW·h = 7.2 × 10^4\space J $，时间 $ t = 180\space s $，实际功率 $ P_{实} = \frac{W}{t} = \frac{7.2 × 10^4\space J}{180\space s} = 400\space W $。由 $ P_{实} = \frac{U_{实}^2}{R_{并}} $ 得实际电压 $ U_{实} = \sqrt{P_{实}R_{并}} = \sqrt{400\space W × 100\space \Omega} = 200\space V $。
(1) $ 0.2\space A $
(2) $ 484\space W $
(3) $ 200\space V $