《2025年精练课堂分层作业九年级数学上册北师大版》

5. 小明想测量电线杆 $ AB $ 的高度,他发现电线杆 $ AB $ 的影子正好落在坡面 $ CD $ 和地面 $ BC $ 上.已知 $ CD $ 和地面成 $ 30° $ 角, $ CD = 4 m $, $ BC = 10 m $,且此时测得 $ 1 m $ 高的标杆在地面上的影长为 $ 2 m $,求 $ AB $ 的长度.

答案： 过D作DE⊥地面于E，在Rt△CDE中，∠DCE=30°，CD=4m。
CE=CD·cos30°=4×(√3/2)=2√3 m，DE=CD·sin30°=4×1/2=2m。
水平总影长BE=BC+CE=10+2√3 m。
设AB=h，由标杆影长比得tanθ=1/2（θ为光线与地面夹角）。
tanθ=(h-DE)/BE=1/2，即(h-2)/(10+2√3)=1/2。
解得h=7+√3。
AB的长度为(7+√3)m。

6. 如图是一个 $ 3 × 8 $ 的网格图,每个小正方形的边长均为 $ 1 $.三个顶点都在小正方形的顶点上的三角形叫作格点三角形.图中格点 $ \triangle ABC $ 的三边长分别为 $ \sqrt{2} $, $ 2 $, $ \sqrt{10} $.请在网格图中画出三个与 $ \triangle ABC $ 相似但不全等的格点三角形,并求与 $ \triangle ABC $ 相似的格点三角形的最大面积.

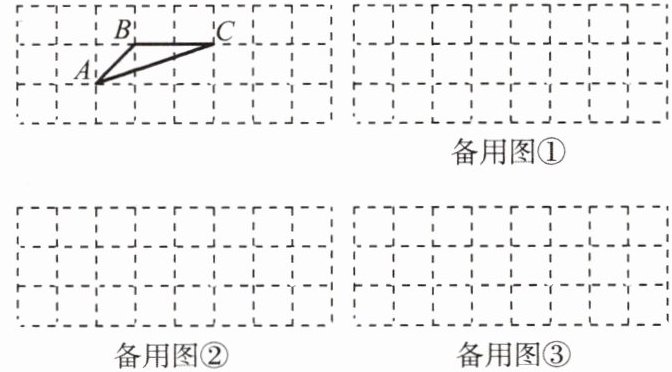
答案： 解答：
一、相似三角形的绘制（以下为三种示例，格点坐标表示）
1. 三角形1（相似比 $ k=\frac{\sqrt{2}}{2} $）：
顶点坐标：$ (0,0) $，$ (1,1) $，$ (2,1) $
三边：$ 1 $，$ \sqrt{2} $，$ \sqrt{5} $（比例 $ 1:\sqrt{2}:\sqrt{5} $）。
2. 三角形2（相似比 $ k=\sqrt{2} $）：
顶点坐标：$ (0,0) $，$ (2,2) $，$ (4,2) $
三边：$ 2 $，$ 2\sqrt{2} $，$ 2\sqrt{5} $（比例 $ 1:\sqrt{2}:\sqrt{5} $）。
3. 三角形3（相似比 $ k=2 $）：
顶点坐标：$ (0,0) $，$ (2,2) $，$ (6,2) $
三边：$ 2\sqrt{2} $，$ 4 $，$ 2\sqrt{10} $（比例 $ 1:\sqrt{2}:\sqrt{5} $）。
二、最大面积计算
原 $ \triangle ABC $ 三边比为 $ 1:\sqrt{2}:\sqrt{5} $，面积为 $ 1 $。相似三角形面积比为相似比的平方。
当相似比 $ k=\sqrt{5} $ 时，三边为 $ \sqrt{10} $，$ 2\sqrt{5} $，$ 5\sqrt{2} $，对应格点坐标 $ (0,0) $，$ (4,2) $，$ (7,1) $，面积为 $ 1 × (\sqrt{5})^2 = 5 $。
最大面积为：$ 5 $
（注：绘制时需在网格图中标出上述坐标对应的格点三角形，此处以坐标描述替代图形。）

7. 如图,四边形 $ ABCD $ 各顶点的坐标分别为 $ A(4,4) $, $ B(6,4) $, $ C(6,6) $, $ D(2,8) $.
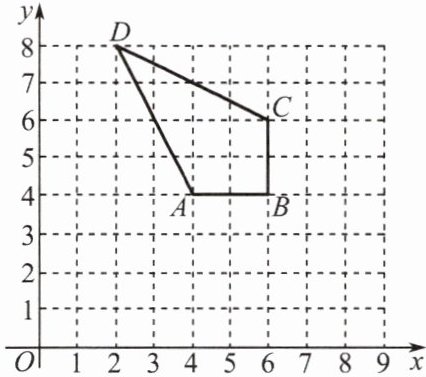
(1) 在第一象限内,画出以原点 $ O $ 为位似中心,与原图的相似比为 $ \frac{1}{2} $ 的位似图形 $ A_1B_1C_1D_1 $ 并写出四边形 $ A_1B_1C_1D_1 $ 的顶点坐标；
(2) 如果四边形 $ ABCD $ 内部有一点 $ P $ 的坐标为 $ (x,y) $,写出点 $ P $ 的对应点 $ P_1 $ 的坐标.

答案：
(1)
根据位似变换性质，以原点$O$为位似中心，相似比为$\frac{1}{2}$，则各点坐标变为原来的一半。
$A_1(2,2)$，$B_1(3,2)$，$C_1(3,3)$，$D_1(1,4)$。
在图中描出各点并依次连接$A_1B_1$，$B_1C_1$，$C_1D_1$，$D_1A_1$。
(2)
因为相似比为$\frac{1}{2}$，点$P(x,y)$的对应点$P_1$的坐标为$(\frac{x}{2},\frac{y}{2})$。

8. 如图,利用直尺、计算机或图形计算器任意画一个 $ \triangle ABC $,以点 $ O $ 为位似中心,自选相似比 $ k $,进行位似变换,得到 $ \triangle A'B'C' $.度量线段 $ OA $, $ OA' $, $ OB $, $ OB' $, $ OC $, $ OC' $ 的长,你有什么发现？任意改变 $ \triangle ABC $ 的位置,得出的结论是否仍然成立？

答案： 设相似比 $k$ 为所选比例（例如 $k = \frac{1}{2}$）。
通过位似变换，得到 $\triangle A'B'C'$。
度量各线段长度：
$OA$ 和 $OA'$，
$OB$ 和 $OB'$，
$OC$ 和 $OC'$。
发现：
$\frac{OA'}{OA} = \frac{OB'}{OB} = \frac{OC'}{OC} = k$（相似比）。
改变 $\triangle ABC$ 的位置后，上述关系仍然成立。
结论：在位似变换中，对应线段的比值等于相似比 $k$。