第76页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
5. 如图,在$\triangle ABC$中,点$D在AB$边上,若$BC= 3$,$BD= 2$,且$\angle BCD= \angle A$,则线段$AD$的长为(

A.2
B.$\dfrac{5}{2}$
C.3
D.$\dfrac{9}{2}$
]
B
)
A.2
B.$\dfrac{5}{2}$
C.3
D.$\dfrac{9}{2}$
]
答案:
B
6. 如图,在$\triangle ABC$中,$\angle C= 90^{ \circ }$,$BC= 8\ {m}$,$AB= 10\ {m}$,点$P从B$点出发,沿$BC方向以2\ {m/s}$的速度移动,点$Q从点C$出发,沿$CA方向以1\ {m/s}$的速度移动.若$P$,$Q同时分别从B$,$C$出发,则经过
]
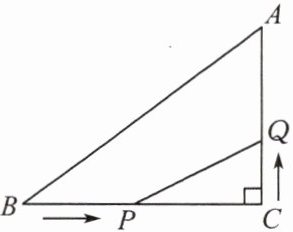
2.4
$s$,$\triangle CPQ \backsim \triangle CBA$.]

答案:
2.4
7. 在$\triangle ABC$中,$P是AB$上的动点($P异于A$,$B$),过点$P的一条直线截\triangle ABC$,使截得的三角形与$\triangle ABC$相似,我们不妨称这种直线为过点$P的\triangle ABC$的相似线.如图,$\angle A= 36^{ \circ }$,$AB= AC$,当点$P在AC$的垂直平分线上时,过点$P的\triangle ABC$的相似线有
]
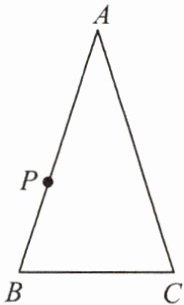
3
条.]

答案:
3
8. 如图,在$Rt \triangle ABC$中,$\angle C= 90^{ \circ }$,$P是BC边上不同于B$,$C$的一动点,过点$P作PQ \perp AB$,垂足为$Q$,连接$AP$.不论点$P在BC$边上何处时,都有
]

$\triangle AQP$
与$\triangle ACB$
相似.]

答案:
$\triangle AQP$,$\triangle ACB$
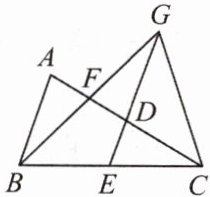
9. 如图,在$\triangle ABC$中,$AC= BC$,点$D$,$E$,$F分别是线段AC$,$BC$,$AD$的中点,$BF$,$ED的延长线交于点G$,连接$GC$.
(1)求证:$AB= GD$.
(2)当$CG= EG$时,求$\dfrac{AC}{AB}$的值.
]
(1)求证:$AB= GD$.
(2)当$CG= EG$时,求$\dfrac{AC}{AB}$的值.
]

答案:
(1)见证明;
(2)√3。
(1)见证明;
(2)√3。
1. 如图,在矩形$ABCD$中,$AB= 3$,$BC= 10$,点$E在BC$边上,$DF \perp AE$,垂足为$F$.若$DF= 6$,则线段$EF$的长为(
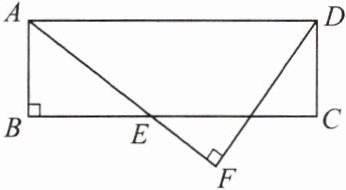
A.2
B.3
C.4
D.5
]
B
)
A.2
B.3
C.4
D.5
]
答案:
B
2. 如图所示,在等腰三角形$ABC$中,$AB= AC$,点$E$,$F在线段BC$上,点$Q在线段AB$上,且$CF= BE$,$AE^{2}= AQ\cdot AB$.求证:
(1)$\angle CAE= \angle BAF$;
(2)$CF\cdot FQ= AF\cdot BQ$.
]

(1)$\angle CAE= \angle BAF$;
(2)$CF\cdot FQ= AF\cdot BQ$.
]

答案:
(1)
∵AB=AC,
∴∠B=∠C(等腰三角形两底角相等)。
∵CF=BE,点C,E,F,B在BC上,
∴CF=CE+EF,BE=BF+EF,
∴CE=BF。
在△AEB和△AFC中,
$\left\{\begin{array}{l} AB=AC \\ ∠B=∠C \\ BE=CF\end{array}\right.$
∴△AEB≌△AFC(SAS),
∴∠BAE=∠CAF。
∴∠BAE-∠EAF=∠CAF-∠EAF,即∠BAF=∠CAE,
∴∠CAE=∠BAF。
(2)
∵AE²=AQ·AB,
∴$\frac{AQ}{AE}=\frac{AE}{AB}$。
又∠QAE=∠BAE(公共角),
∴△AQE∽△AEB(两边成比例且夹角相等的两个三角形相似)。
∴∠AQE=∠AEB。
∵∠AQE=∠BQF(对顶角相等),
∴∠AEB=∠BQF。
在△AEB和△BQF中,∠AEB=∠BQF,∠B=∠B,
∴∠BAE=∠BFQ。
由
(1)△AEB≌△AFC得∠BAE=∠CAF,
∴∠BFQ=∠CAF。
在△BFQ和△CAF中,∠B=∠C,∠BFQ=∠CAF,
∴△BFQ∽△CAF(两角分别相等的两个三角形相似)。
∴$\frac{BQ}{CF}=\frac{FQ}{AF}$,
∴CF·FQ=AF·BQ。
(1)
∵AB=AC,
∴∠B=∠C(等腰三角形两底角相等)。
∵CF=BE,点C,E,F,B在BC上,
∴CF=CE+EF,BE=BF+EF,
∴CE=BF。
在△AEB和△AFC中,
$\left\{\begin{array}{l} AB=AC \\ ∠B=∠C \\ BE=CF\end{array}\right.$
∴△AEB≌△AFC(SAS),
∴∠BAE=∠CAF。
∴∠BAE-∠EAF=∠CAF-∠EAF,即∠BAF=∠CAE,
∴∠CAE=∠BAF。
(2)
∵AE²=AQ·AB,
∴$\frac{AQ}{AE}=\frac{AE}{AB}$。
又∠QAE=∠BAE(公共角),
∴△AQE∽△AEB(两边成比例且夹角相等的两个三角形相似)。
∴∠AQE=∠AEB。
∵∠AQE=∠BQF(对顶角相等),
∴∠AEB=∠BQF。
在△AEB和△BQF中,∠AEB=∠BQF,∠B=∠B,
∴∠BAE=∠BFQ。
由
(1)△AEB≌△AFC得∠BAE=∠CAF,
∴∠BFQ=∠CAF。
在△BFQ和△CAF中,∠B=∠C,∠BFQ=∠CAF,
∴△BFQ∽△CAF(两角分别相等的两个三角形相似)。
∴$\frac{BQ}{CF}=\frac{FQ}{AF}$,
∴CF·FQ=AF·BQ。
查看更多完整答案,请扫码查看


