第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1. 国家统计局统计数据显示, 我国快递业务收入逐年增加, 2017 年至 2019 年我国快递业务收入由 5 000 亿元增加到 7 500 亿元. 设我国 2017 年至 2019 年快递业务收入的年平均增长率为 $ x $, 则可列方程 (
A.$ 5\ 000(1 + 2x) = 7\ 500 $
B.$ 5\ 000×2(1 + x) = 7\ 500 $
C.$ 5\ 000(1 + x)^2 = 7\ 500 $
D.$ 5\ 000 + 5\ 000(1 + x) + 5\ 000(1 + x)^2 = 7\ 500 $
C
)A.$ 5\ 000(1 + 2x) = 7\ 500 $
B.$ 5\ 000×2(1 + x) = 7\ 500 $
C.$ 5\ 000(1 + x)^2 = 7\ 500 $
D.$ 5\ 000 + 5\ 000(1 + x) + 5\ 000(1 + x)^2 = 7\ 500 $
答案:
C
2. 某种药品原价每盒 60 元, 由于医疗政策改革, 价格经过两次下调后现在售价每盒 48.6 元, 则平均每次下调的百分率为
10%
.
答案:
$10\%$
3. 某书店将每本成本为 30 元的一批图书, 以 40 元的单价出售时, 每天的销售量是 300 本. 已知在每本涨价幅度不超过 10 元的情况下, 若每本涨价 1 元, 则每天就会少售出 10 本, 设每本书上涨了 $ x $ 元. 请解答以下问题:
(1) 每天可售出书
(2) 若书店想通过售出这批图书每天获得 3 750 元的利润, 应涨价多少元?
(1) 每天可售出书
$300 - 10x$
本(用含 $ x $ 的代数式表示);(2) 若书店想通过售出这批图书每天获得 3 750 元的利润, 应涨价多少元?
答案:
(1) $300 - 10x$
(2)
根据总利润$=$每本利润$×$销售数量,可列出方程:
$(40 - 30 + x)(300 - 10x) = 3750$
即:
$(10 + x)(300 - 10x) = 3750$
展开得:
$3000-100x+300x-10x^2=3750$
整理得:
$-10x^2 + 200x - 750 = 0$
两边同时除以$-10$,得:
$x^2 - 20x + 75 = 0$
因式分解得:
$(x-5)(x-15)=0$
解得:
$x_1 = 5$,$x_2 = 15$
因为每本涨价幅度不超过$10$元,即$0\leq x\leq10$,所以$x = 15$不合题意,舍去。
答:应涨价$5$元。
(1) $300 - 10x$
(2)
根据总利润$=$每本利润$×$销售数量,可列出方程:
$(40 - 30 + x)(300 - 10x) = 3750$
即:
$(10 + x)(300 - 10x) = 3750$
展开得:
$3000-100x+300x-10x^2=3750$
整理得:
$-10x^2 + 200x - 750 = 0$
两边同时除以$-10$,得:
$x^2 - 20x + 75 = 0$
因式分解得:
$(x-5)(x-15)=0$
解得:
$x_1 = 5$,$x_2 = 15$
因为每本涨价幅度不超过$10$元,即$0\leq x\leq10$,所以$x = 15$不合题意,舍去。
答:应涨价$5$元。
1. 某件羊毛衫的售价为 1 000 元, 因换季促销, 商家决定降价销售, 在连续两次降价 $ x\% $ 后, 售价降低了 190 元, 则 $ x $ 为(
A.5
B.10
C.19
D.81
B
)A.5
B.10
C.19
D.81
答案:
B
2. 一件工艺品进价为 100 元, 标价 130 元售出, 每天平均可售出 100 件. 根据销售统计, 一件工艺品每降价 1 元出售, 则每天可多售出 5 件. 某店为减少库存量, 同时使每天平均获得的利润为 3 000 元, 每件需降价(
A.12 元
B.10 元
C.8 元
D.5 元
B
)A.12 元
B.10 元
C.8 元
D.5 元
答案:
B
3. 有 $ m $ 支球队参加篮球比赛, 共比赛了 21 场, 每两队之间都比赛一场, 则下列方程中符合题意的是(
A.$ \frac{1}{2}m(m - 1) = 21 $
B.$ \frac{1}{2}m(m + 1) = 21 $
C.$ m(m - 1) = 21 $
D.$ m(m + 1) = 21 $
A
)A.$ \frac{1}{2}m(m - 1) = 21 $
B.$ \frac{1}{2}m(m + 1) = 21 $
C.$ m(m - 1) = 21 $
D.$ m(m + 1) = 21 $
答案:
A
4. 某厂家 2023 年 1—5 月份的口罩产量统计如图所示. 设从 2—4 月份该厂家口罩产量的平均月增长率为 $ x $, 根据题意可得方程(
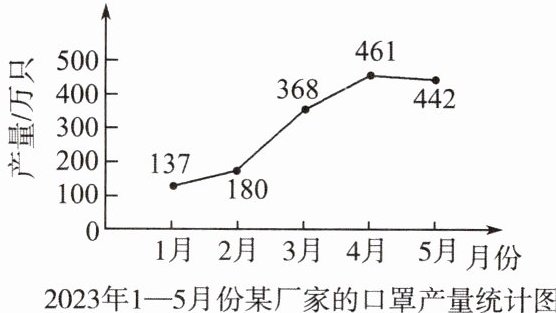
A.$ 180(1 - x)^2 = 461 $
B.$ 180(1 + x)^2 = 461 $
C.$ 368(1 - x)^2 = 442 $
D.$ 368(1 + x)^2 = 442 $
B
)
A.$ 180(1 - x)^2 = 461 $
B.$ 180(1 + x)^2 = 461 $
C.$ 368(1 - x)^2 = 442 $
D.$ 368(1 + x)^2 = 442 $
答案:
B
5. 一个两位数, 十位数字与个位数字之和为 9, 且这两个数字之积等于它们两个数字和的 2 倍, 则这个两位数是(
A.36
B.63
C.36 或 63
D.-36 或 -63
C
)A.36
B.63
C.36 或 63
D.-36 或 -63
答案:
C
查看更多完整答案,请扫码查看


