第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
16. 已知一元二次方程 $ x^{2}+x - 1 = 0 $,嘉淇在探究该方程时,得到以下结论:
① 该方程有两个不相等的实数根;② 该方程有一个根为 1;③ 该方程的根是整数;④ 该方程有一个根小于 -1。
其中正确结论的序号为(
A.①③
B.②④
C.①④
D.②③
① 该方程有两个不相等的实数根;② 该方程有一个根为 1;③ 该方程的根是整数;④ 该方程有一个根小于 -1。
其中正确结论的序号为(
C
)A.①③
B.②④
C.①④
D.②③
答案:
C
17. 已知实数 $ a $,$ b $ 是方程 $ x^{2}-x - 1 = 0 $ 的两根,则 $ \frac{b}{a}+\frac{a}{b} $ 的值为
-3
。
答案:
-3
18. 若 $ (x^{2}+y^{2})^{2}-5(x^{2}+y^{2})-6 = 0 $,则 $ x^{2}+y^{2}= $
6
。
答案:
6
19. 已知两个连续奇数的积是 63,则下列各数中,是这两个数中的一个的是(
A.-11
B.6
C.9
D.11
C
)A.-11
B.6
C.9
D.11
答案:
C
20. 某县计划用三年时间对全县学校的设施和设备进行全面改造,2023 年县政府已投资 5 亿元人民币,若每年投资的增长率相同,预计 2025 年投资 7.2 亿元人民币,那么每年投资的增长率为(
A.20%
B.40%
C.-20%
D.30%
A
)A.20%
B.40%
C.-20%
D.30%
答案:
A
21. 四个相等的矩形(每一个矩形的面积都是 35)拼成一个大正方形,如图所示。利用所给的数据,能得到的方程是(
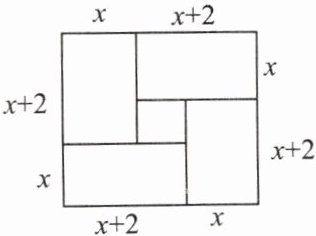
A.$ x(x + 2)= 35 $
B.$ x(x + 2)= 35 + 4 $
C.$ x(x + 2)= 4 × 35 $
D.$ x(x + 2)= 4 × 35 + 4 $
A
)
A.$ x(x + 2)= 35 $
B.$ x(x + 2)= 35 + 4 $
C.$ x(x + 2)= 4 × 35 $
D.$ x(x + 2)= 4 × 35 + 4 $
答案:
A
22. 某年级举办篮球友谊赛,参赛的每两个队之间都要比赛一场,共要比赛 36 场,则参加此次比赛的球队数是(
A.6
B.7
C.8
D.9
D
)A.6
B.7
C.8
D.9
答案:
D
23. 如图,将一块正方形空地划出部分区域进行绿化,原空地一边减少了 2 m,另一边减少了 3 m,剩余一块面积为 20 m^2 的矩形空地,设原正方形空地的边长为 $ x $ m,则下列方程正确的是(
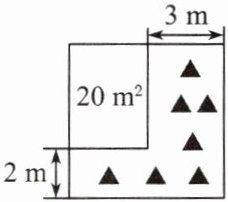
A.$ (x - 3)(x - 2)= 20 $
B.$ (x + 3)(x + 2)= 20 $
C.$ x^{2}-3x - 2x = 20 $
D.$ x^{2}-3 × 2 = 20 $
A
)
A.$ (x - 3)(x - 2)= 20 $
B.$ (x + 3)(x + 2)= 20 $
C.$ x^{2}-3x - 2x = 20 $
D.$ x^{2}-3 × 2 = 20 $
答案:
A
24. 在毕业前夕,九年级某班每名同学都为其他同学写了一段毕业感言,全班共写了 2256 段毕业感言。如果该班有 $ x $ 名同学,根据题意列出方程为
$x(x-1)=2256$
。
答案:
$x(x-1)=2256$
25. 如图,$ AB \perp BC $,$ AB = 10 $ cm,点 $ M $ 以每秒 1 cm 的速度从点 $ A $ 开始沿 $ AB $ 边向点 $ B $ 移动,点 $ N $ 以每秒 2 cm 的速度从点 $ B $ 开始沿 $ BC $ 边向点 $ C $ 运动,求使 $ \triangle MBN $ 的面积等于 24 cm^2 时,点 $ M $ 运动的时间。设所求的运动时间为 $ t $ 秒,列出的方程是
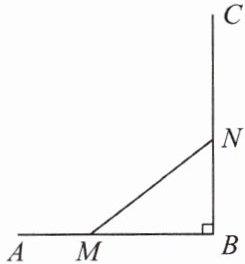
$ t^2 - 10t + 24 = 0 $
。
答案:
$ t^2 - 10t + 24 = 0 $
查看更多完整答案,请扫码查看


