《2025年精练课堂分层作业九年级数学上册北师大版》

6. 如图,在五角星中,点C是AB的黄金分割点.已知AB= 8,则DC= 8√5 - 16.
]

答案： 8√5 - 16

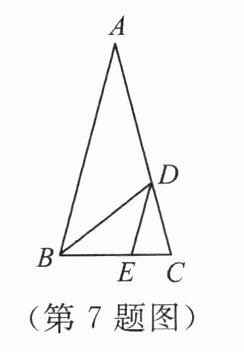
7. 如图,△ABC是顶角为36°的等腰三角形,若△ABC,△BDC,△DEC都是黄金三角形(底与腰的比为$\frac{\sqrt{5}-1}{2}$的三角形是黄金三角形).已知AB= 4,则DE= $6-2\sqrt{5}$.
]

答案： $6-2\sqrt{5}$

8. 如图,在矩形ABCD(AB＜BC)中,如果$\frac{AB}{BC}= \frac{\sqrt{5}-1}{2}$,那么称这个矩形为黄金矩形.在黄金矩形ABCD内作正方形CDEF,得到一个小矩形ABFE.请问矩形ABFE是否为黄金矩形？请说明理由.
]

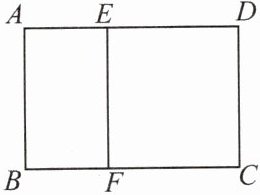
答案： 矩形ABFE是黄金矩形。理由如下：
设$BC = x$，
∵矩形$ABCD$为黄金矩形，且$AB ＜ BC$，
∴$\frac{AB}{BC} = \frac{\sqrt{5}-1}{2}$，则$AB = \frac{\sqrt{5}-1}{2}x$。
∵四边形$CDEF$是正方形，
∴$CD = CF = AB = \frac{\sqrt{5}-1}{2}x$。
在矩形$ABFE$中，$BF = BC - CF = x - \frac{\sqrt{5}-1}{2}x = \frac{2x - (\sqrt{5}-1)x}{2} = \frac{(3 - \sqrt{5})x}{2}$，$AB = \frac{\sqrt{5}-1}{2}x$。
∵$AB ＜ BC$，$\frac{\sqrt{5}-1}{2} \approx 0.618$，$\frac{3 - \sqrt{5}}{2} \approx 0.382$，
∴$BF ＜ AB$，矩形$ABFE$的较短边为$BF$，较长边为$AB$。
计算$\frac{BF}{AB}$：
$\frac{BF}{AB} = \frac{\frac{(3 - \sqrt{5})x}{2}}{\frac{(\sqrt{5}-1)x}{2}} = \frac{3 - \sqrt{5}}{\sqrt{5}-1} = \frac{(3 - \sqrt{5})(\sqrt{5}+1)}{(\sqrt{5}-1)(\sqrt{5}+1)} = \frac{2\sqrt{5}-2}{4} = \frac{\sqrt{5}-1}{2}$
即$\frac{BF}{AB} = \frac{\sqrt{5}-1}{2}$，且$BF ＜ AB$，
∴矩形$ABFE$是黄金矩形。
结论：矩形$ABFE$是黄金矩形。

如图,顶角为36°的等腰三角形,其底边与腰之比等于k,这样的三角形被称为黄金三角形.已知腰AB= 1,△ABC为第一个黄金三角形,△BCD为第二个黄金三角形,△CDE为第三个黄金三角形,以此类推,第2020个黄金三角形的周长为(D)

A.$k^{2018}$
B.$k^{2019}$
C.$\frac{k^{2018}}{2 + k}$
D.$k^{2019}(2 + k)$
]

答案： D