第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
3. 在甲、乙两个不透明的口袋中,分别有4个和3个大小、材质完全相同的小球,其中甲口袋中的小球上分别标有数字0,1,2,3,乙口袋中的小球上分别标有数字1,2,3.先从甲口袋中随机摸出一个小球,记下数字为m,再从乙口袋中随机摸出一个小球,记下数字为n.
(1) 请用列表或画树状图的方法表示出所有(m,n)可能的结果;
(2) 规定:若m,n都是方程$x^{2}-3x+2= 0$的解,则小明获胜;若m,n都不是方程$x^{2}-3x+2= 0$的解,则小宇获胜.问他们两人谁获胜的概率大?
(1) 请用列表或画树状图的方法表示出所有(m,n)可能的结果;
(2) 规定:若m,n都是方程$x^{2}-3x+2= 0$的解,则小明获胜;若m,n都不是方程$x^{2}-3x+2= 0$的解,则小宇获胜.问他们两人谁获胜的概率大?
答案:
(1) 列表如下:
| m\n | 1 | 2 | 3 |
|-----|---|---|---|
| 0 | (0,1) | (0,2) | (0,3) |
| 1 | (1,1) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,3) |
所有可能结果为:(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共12种。
(2) 解方程$x^2 - 3x + 2 = 0$,因式分解得$(x - 1)(x - 2) = 0$,解得$x = 1$或$x = 2$,即方程的解为1,2。
小明获胜条件:$m,n$都是方程的解,即$m \in \{1,2\}$且$n \in \{1,2\}$。满足条件的结果有(1,1),(1,2),(2,1),(2,2),共4种。$P(小明) = \frac{4}{12} = \frac{1}{3}$。
小宇获胜条件:$m,n$都不是方程的解,即$m \in \{0,3\}$且$n = 3$。满足条件的结果有(0,3),(3,3),共2种。$P(小宇) = \frac{2}{12} = \frac{1}{6}$。
因为$\frac{1}{3} > \frac{1}{6}$,所以小明获胜的概率大。
答:小明获胜的概率大。
(1) 列表如下:
| m\n | 1 | 2 | 3 |
|-----|---|---|---|
| 0 | (0,1) | (0,2) | (0,3) |
| 1 | (1,1) | (1,2) | (1,3) |
| 2 | (2,1) | (2,2) | (2,3) |
| 3 | (3,1) | (3,2) | (3,3) |
所有可能结果为:(0,1),(0,2),(0,3),(1,1),(1,2),(1,3),(2,1),(2,2),(2,3),(3,1),(3,2),(3,3),共12种。
(2) 解方程$x^2 - 3x + 2 = 0$,因式分解得$(x - 1)(x - 2) = 0$,解得$x = 1$或$x = 2$,即方程的解为1,2。
小明获胜条件:$m,n$都是方程的解,即$m \in \{1,2\}$且$n \in \{1,2\}$。满足条件的结果有(1,1),(1,2),(2,1),(2,2),共4种。$P(小明) = \frac{4}{12} = \frac{1}{3}$。
小宇获胜条件:$m,n$都不是方程的解,即$m \in \{0,3\}$且$n = 3$。满足条件的结果有(0,3),(3,3),共2种。$P(小宇) = \frac{2}{12} = \frac{1}{6}$。
因为$\frac{1}{3} > \frac{1}{6}$,所以小明获胜的概率大。
答:小明获胜的概率大。
4. 在一个不透明的盒子里装着只有颜色不同的黑、白两种球共30个.小鲍做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个记下颜色,再把它放回盒子中,不断重复上述过程.下图是“摸到白色球”的频率折线统计图.
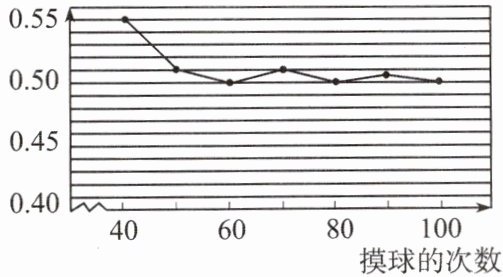
(1) 当n很大时,摸到白球的频率将会接近
(2) 如果要使摸到白球的概率为$\frac{3}{4}$,需要往盒子里再放入多少个白球?

(1) 当n很大时,摸到白球的频率将会接近
0.50
(精确到0.01),估计盒子里白球有______15
个,假如摸一次球,摸到白球的概率约为______0.50
;(2) 如果要使摸到白球的概率为$\frac{3}{4}$,需要往盒子里再放入多少个白球?
答案:
(1)
根据频率折线统计图,当$n$很大时,摸到白球的频率将会接近$0.50$;
估计盒子里白球有$30×0.50 = 15$个;
假如摸一次球,摸到白球的概率约为$0.50$。
(2)
设再放入$x$个白球,由题意得$\frac{15 + x}{30 + x}=\frac{3}{4}$,
$4(15 + x)=3(30 + x)$,
$60+4x = 90+3x$,
$4x - 3x=90 - 60$,
解得$x = 30$。
答:
(1) $0.50$,$15$,$0.50$;
(2) 需要往盒子里再放入$30$个白球。
(1)
根据频率折线统计图,当$n$很大时,摸到白球的频率将会接近$0.50$;
估计盒子里白球有$30×0.50 = 15$个;
假如摸一次球,摸到白球的概率约为$0.50$。
(2)
设再放入$x$个白球,由题意得$\frac{15 + x}{30 + x}=\frac{3}{4}$,
$4(15 + x)=3(30 + x)$,
$60+4x = 90+3x$,
$4x - 3x=90 - 60$,
解得$x = 30$。
答:
(1) $0.50$,$15$,$0.50$;
(2) 需要往盒子里再放入$30$个白球。
5. 某校为研究学生的课余爱好情况,采取抽样调查的方法,从运动、娱乐、阅读、上网四个方面调查了若干学生,并将调查的结果绘制成下图中两幅不完整的统计图.请你根据图中提供的信息解答下列问题:
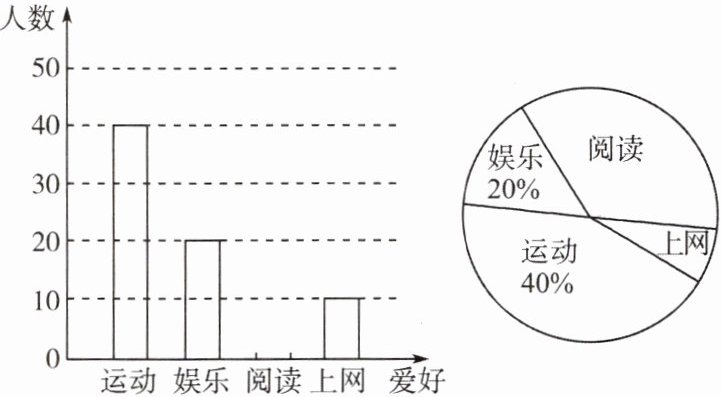
(1) 在这次研究中,一共调查了
(2) 补全条形统计图,并计算“阅读”部分的圆心角;
(3) 在全校学生中随机选出一名学生参加演讲比赛,用频率估计概率,求选出的恰好是爱好阅读的学生的概率.

(1) 在这次研究中,一共调查了
100
名学生,若该校共有1500名学生,估计全校爱好运动的学生共有______600
名;(2) 补全条形统计图,并计算“阅读”部分的圆心角;
(3) 在全校学生中随机选出一名学生参加演讲比赛,用频率估计概率,求选出的恰好是爱好阅读的学生的概率.
答案:
(1)
调查学生总数:从扇形统计图知爱好娱乐的学生占$20\%$,从条形统计图知爱好娱乐的学生有$20$人,所以总人数为$20÷20\% = 100$名。
爱好运动的学生数:$1500×40\% = 600$名。
(2)
爱好阅读的人数:总人数为$100$人,爱好运动$40$人,爱好娱乐$20$人,爱好上网$10$人,所以爱好阅读的人数为$100 - 40 - 20 - 10 = 30$人。
补全条形统计图(图略,在阅读对应位置画高度为$30$的直条)。
“阅读”部分的圆心角:$360^{\circ}×\frac{30}{100}=108^{\circ}$。
(3)
爱好阅读的学生的频率为$\frac{30}{100}=0.3$,用频率估计概率,选出的恰好是爱好阅读的学生的概率为$0.3$。
故答案依次为:(1)$100$;$600$;(2)补全条形统计图(图略);$108^{\circ}$;(3)$0.3$。
调查学生总数:从扇形统计图知爱好娱乐的学生占$20\%$,从条形统计图知爱好娱乐的学生有$20$人,所以总人数为$20÷20\% = 100$名。
爱好运动的学生数:$1500×40\% = 600$名。
(2)
爱好阅读的人数:总人数为$100$人,爱好运动$40$人,爱好娱乐$20$人,爱好上网$10$人,所以爱好阅读的人数为$100 - 40 - 20 - 10 = 30$人。
补全条形统计图(图略,在阅读对应位置画高度为$30$的直条)。
“阅读”部分的圆心角:$360^{\circ}×\frac{30}{100}=108^{\circ}$。
(3)
爱好阅读的学生的频率为$\frac{30}{100}=0.3$,用频率估计概率,选出的恰好是爱好阅读的学生的概率为$0.3$。
故答案依次为:(1)$100$;$600$;(2)补全条形统计图(图略);$108^{\circ}$;(3)$0.3$。
查看更多完整答案,请扫码查看


