第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
4. 如图,球从 $ A $ 处射出,经球台边挡板 $ CD $ 反射到点 $ B $,已知 $ AC = 10\ cm $, $ BD = 15\ cm $, $ CD = 50\ cm $,则点 $ E $ 到点 $ C $ 的距离是

20
$ cm $。
答案:
$20$
5. 一种测量小管口径的量具如图所示, $ AB $ 长为 $ 12\ cm $, $ AE $ 被分成 $ 60 $ 等份。若小管口径 $ DE $ 正好对着量具上 $ 40 $ 份处( $ DE // AB $),则小管口径 $ DE $ 的长是

8
。
答案:
8
6. 如图,测得边 $ DF $ 离地面的高度为 $ 1.4\ m $,点 $ D $ 到 $ AB $ 的距离等于 $ 6\ m $。已知 $ DF = 30\ cm $, $ EF = 20\ cm $,那么树 $ AB $ 的高度等于
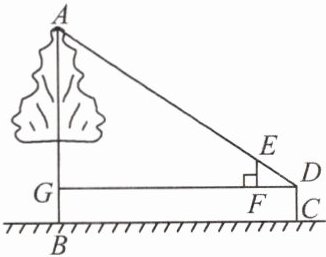
5.6
$ m $。
答案:
5.6
7. 如图, $ AB $ 表示一个窗户的高, $ AE $ 和 $ BD $ 表示射入室内的光线,窗户的下端到地面的距离 $ BC = 1.2\ m $。已知某一时刻 $ BC $ 在地面的影长 $ CD = 1.8\ m $, $ AC $ 在地面的影长 $ CE = 4.8\ m $,则窗户的高度 $ AB = $

2
$ m $。
答案:
2
8. 为了测量一棵大树的高度,准备了如下测量工具:①镜子;②皮尺;③长为 $ 2\ m $ 的标杆;④高为 $ 1.5\ m $ 的测角仪。请根据你所设计的测量方案,回答下列问题:
(1)在你设计的方案中,选用的测量工具是
(2)画出测量方案示意图;
(3)你需要测量示意图中哪些数据,并用 $ a $, $ b $, $ c $, $ \alpha $, $ \beta $ 等字母表示测得的数据;
(4)写出求树高的算式: $ AB = $
(1)在你设计的方案中,选用的测量工具是
②④
;(填序号)(2)画出测量方案示意图;
(3)你需要测量示意图中哪些数据,并用 $ a $, $ b $, $ c $, $ \alpha $, $ \beta $ 等字母表示测得的数据;
(4)写出求树高的算式: $ AB = $
$\frac{a\tan\alpha\tan\beta}{\tan\alpha - \tan\beta}+1.5$
$ m $。(用 $ a $, $ b $, $ c $, $ \alpha $, $ \beta $ 等字母表示)
答案:
$(1)$ 选用测量工具
选用的测量工具是:②皮尺、④高为$1.5m$的测角仪。
$(2)$ 测量方案示意图
示意图为:在平地上选取一点$C$,用测角仪在点$C$处测得树顶$A$的仰角$\angle ADE=\alpha$,然后沿直线$BC$后退$m$米到点$F$,再测得树顶$A$的仰角$\angle AGE = \beta$(示意图略,可根据描述自行绘制简单图形,包含树$AB$、测角仪、测量点等元素)。
$(3)$ 测量数据
需要测量的数据:测角仪的高$CD = EF = 1.5m$,$CF = a$(即后退的距离),$\angle ADE=\alpha$,$\angle AGE=\beta$。
$(4)$ 求树高算式
设$DG = x$,在$Rt\triangle ADG$中,$\tan\alpha=\frac{AG}{DG}$,则$AG = DG\tan\alpha=x\tan\alpha$;
在$Rt\triangle AFG$中,$\tan\beta=\frac{AG}{FG}$,$FG=DG + DF=x + a$,则$AG=(x + a)\tan\beta$。
所以$x\tan\alpha=(x + a)\tan\beta$,
$x\tan\alpha=x\tan\beta+a\tan\beta$,
$x(\tan\alpha-\tan\beta)=a\tan\beta$,
解得$x = \frac{a\tan\beta}{\tan\alpha-\tan\beta}$。
那么$AB = AG+GB= x\tan\alpha + 1.5=\frac{a\tan\alpha\tan\beta}{\tan\alpha-\tan\beta}+ 1.5$。
综上,答案依次为: $(1)$ $\boldsymbol{②④}$;$(4)$ $\boldsymbol{\frac{a\tan\alpha\tan\beta}{\tan\alpha - \tan\beta}+1.5}$ 。
选用的测量工具是:②皮尺、④高为$1.5m$的测角仪。
$(2)$ 测量方案示意图
示意图为:在平地上选取一点$C$,用测角仪在点$C$处测得树顶$A$的仰角$\angle ADE=\alpha$,然后沿直线$BC$后退$m$米到点$F$,再测得树顶$A$的仰角$\angle AGE = \beta$(示意图略,可根据描述自行绘制简单图形,包含树$AB$、测角仪、测量点等元素)。
$(3)$ 测量数据
需要测量的数据:测角仪的高$CD = EF = 1.5m$,$CF = a$(即后退的距离),$\angle ADE=\alpha$,$\angle AGE=\beta$。
$(4)$ 求树高算式
设$DG = x$,在$Rt\triangle ADG$中,$\tan\alpha=\frac{AG}{DG}$,则$AG = DG\tan\alpha=x\tan\alpha$;
在$Rt\triangle AFG$中,$\tan\beta=\frac{AG}{FG}$,$FG=DG + DF=x + a$,则$AG=(x + a)\tan\beta$。
所以$x\tan\alpha=(x + a)\tan\beta$,
$x\tan\alpha=x\tan\beta+a\tan\beta$,
$x(\tan\alpha-\tan\beta)=a\tan\beta$,
解得$x = \frac{a\tan\beta}{\tan\alpha-\tan\beta}$。
那么$AB = AG+GB= x\tan\alpha + 1.5=\frac{a\tan\alpha\tan\beta}{\tan\alpha-\tan\beta}+ 1.5$。
综上,答案依次为: $(1)$ $\boldsymbol{②④}$;$(4)$ $\boldsymbol{\frac{a\tan\alpha\tan\beta}{\tan\alpha - \tan\beta}+1.5}$ 。
1. 如图,在一块斜边长 $ 30\ cm $ 的直角三角形木板( $ Rt \triangle ACB $)上截取一个正方形 $ CDEF $,点 $ D $ 在边 $ BC $ 上,点 $ E $ 在斜边 $ AB $ 上,点 $ F $ 在边 $ AC $ 上。若 $ AF:AC = 1:3 $,则这块木板截取正方形 $ CDEF $ 后,剩余部分的面积为 (
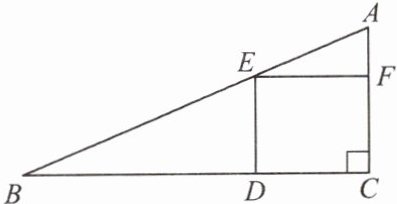
A.$ 100\ cm^2 $
B.$ 150\ cm^2 $
C.$ 170\ cm^2 $
D.$ 200\ cm^2 $
A
)
A.$ 100\ cm^2 $
B.$ 150\ cm^2 $
C.$ 170\ cm^2 $
D.$ 200\ cm^2 $
答案:
A
2. 如图①,长、宽均为 $ 3 $,高为 $ 8 $ 的长方体容器,放置在水平桌面上,里面盛有水,水面高为 $ 6 $。绕底面一棱进行旋转倾斜后,水面恰好触到容器口边缘,图②是此时的示意图,求图②中水面的高度。


答案:
4
查看更多完整答案,请扫码查看


