《2025年精练课堂分层作业九年级数学上册北师大版》

6. 已知 2 是关于 x 的方程 $ x^{2} - 2mx + 3m = 0 $ 的一个根,并且这个方程的两个根恰好是等腰三角形 ABC 的两条边长,则三角形 ABC 的周长为(B)
A.10
B.14
C.10 或 14
D.8 或 10

答案： B

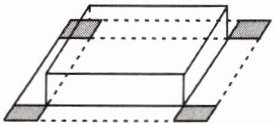
7. 如图,有一块长 20 cm、宽 10 cm 的矩形铁皮,如果在铁皮的四个角上截去四个相同的小正方形,然后把四边折起来,做成一个底面面积为$ 96 cm^2 $的无盖的盒子,那么这个盒子的容积为192.

答案： 192

8. 如图,小明家有一块长 1.50 m、宽 1 m 的矩形地毯,为了使地毯美观,爸爸请来工匠在地毯的四周镶上宽度相同的花色地毯,镶完后地毯的面积是原地毯面积的 2 倍,则花色地毯的宽为0.25m.

答案： 0.25

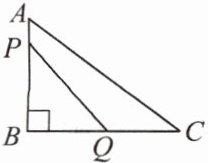
9. 如图,在 Rt△ABC 中,$ ∠B = 90^{\circ} $,$ AC = 10 $ cm,$ BC = 8 $ cm.现有两个动点 P,Q 分别从点 A 和点 B 同时出发,其中点 P 以 1 cm/s 的速度沿 AB 向终点 B 移动；点 Q 以 2 cm/s 的速度沿 BC 向终点 C 移动,其中一点到达终点,另一点也随之停止.连接 PQ,若经 x 秒后,P,Q 两点之间的距离为 $ 4\sqrt{2} $,那么 x 的值为2或0.4.

答案： $2$或$0.4$（若题目要求填单个答案格式，本题应按题目要求呈现，由于这里不是选择形式，按求根结果呈现）若按填空题理解，答案为$2$或$0.4$ 。

10. 一个矩形的周长为 56 cm.
(1)当矩形面积为$ 180 cm^2 $时,长、宽分别为多少？
(2)能围成面积为$ 200 cm^2 $的矩形吗？请说明理由.

答案：
(1) 设长为 $x$ cm，则宽为 $(28 - x)$ cm（因为周长为56cm，所以长加宽为28cm）。
根据题意，面积 $S = x(28 - x) = 180$。
展开得：$x^2 - 28x + 180 = 0$。
解此方程，使用公式法：
$x = \frac{28 \pm \sqrt{(-28)^2 - 4 × 1 × 180}}{2 × 1}$
$x = \frac{28 \pm \sqrt{784 - 720}}{2}$
$x = \frac{28 \pm \sqrt{64}}{2}$
$x = \frac{28 \pm 8}{2}$
得到两个解：$x_1 = 18, x_2 = 10$。
由于 $x ＞ 28 - x$，所以长为18cm，宽为10cm。
答：长为18cm，宽为10cm。
(2) 设长为 $x$ cm，则宽为 $(28 - x)$ cm。
根据题意，假设面积 $S = x(28 - x) = 200$。
展开得：$x^2 - 28x + 200 = 0$。
使用判别式判断方程是否有实数解：
$\Delta = (-28)^2 - 4 × 1 × 200 = 784 - 800 = -16 ＜ 0$。
因为 $\Delta ＜ 0$，所以方程无实数解。
答：不能围成面积为 $200 cm^2$ 的矩形。

小明家有一块长 8 m、宽 6 m 的矩形空地,妈妈准备在该空地上建造一个花园,并使花园面积为矩形空地面积的一半.小明设计了下图中的四种方案供妈妈挑选,请你选择其中的一种方案帮小明求出图中的 x 值.
]

答案： 选择方案二：
矩形空地面积：$8×6=48\,m^2$，花园面积：$48×\frac{1}{2}=24\,m^2$。
由方案二可知，花园为矩形，长为$(8-2x)\,m$，宽为$(6-2x)\,m$。
根据题意，得$(8-2x)(6-2x)=24$。
整理得：$4x^2 - 28x + 24=0$，即$x^2 - 7x + 6=0$。
$a=1$，$b=-7$，$c=6$。
$\Delta=b^2 - 4ac=(-7)^2 - 4×1×6=49 - 24=25$。
$x=\frac{-b\pm\sqrt{\Delta}}{2a}=\frac{7\pm\sqrt{25}}{2}=\frac{7\pm5}{2}$。
$x_1=\frac{7+5}{2}=6$（不合题意，舍去），$x_2=\frac{7-5}{2}=1$。
所以$x=1$。