《2025年精练课堂分层作业九年级数学上册北师大版》

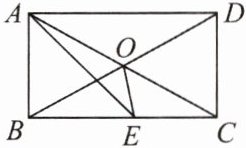
4. 如图,在矩形$ABCD$中,$AE平分\angle BAD$,$\angle CAE = 15^{\circ}$,那么$\angle BOE$的度数为75°.

答案： 75°

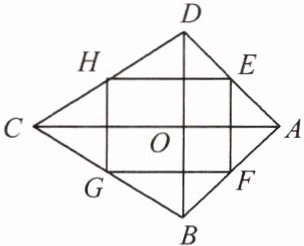
5. 如图所示,在四边形$ABCD$中,对角线$AC\perp BD$,垂足为$O$,点$E$,$F$,$G$,$H分别为边AD$,$AB$,$BC$,$CD$的中点.若$AC = 8$,$BD = 6$,则四边形$EFGH$的面积为12.

答案： 12

6. 如图所示,已知矩形$ABCD$,连接$BD$,延长矩形$ABCD的边BC至点E$,使$CE = BD$,连接$AE$,如果$\angle ADB = 30^{\circ}$,那么$\angle E = $15°.

答案： 15°

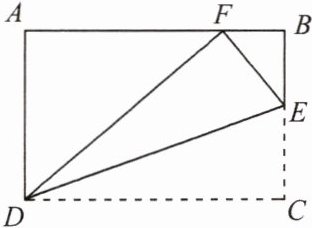
7. 如图,在矩形$ABCD$中,$AB = 10$,$AD = 6$,$E为BC$上一点,把$\triangle CDE沿DE$折叠,使点$C落在AB边上的F$处,则$CE$的长为$\frac{10}{3}$.

答案： $\frac{10}{3}$（或填$3.33$附近准确分数值 ）*（按照题目要求这里应写分数形式$\frac{10}{3}$ ）

8. 如图,菱形$ABCD的对角线AC$,$BD相交于点O$,$E是AD$的中点,点$F$,$G在AB$上,$EF\perp AB$,$OG// EF$.
(1) 求证:四边形$OEFG$是矩形;
(2) 若$AD = 10$,$EF = 4$,求$OE和BG$的长.

答案：
(1)证明：
∵菱形$ABCD$，对角线$AC$、$BD$交于点$O$，
∴$O$为$BD$中点，$AB=AD$。
∵$E$是$AD$中点，
∴$OE$是$\triangle ABD$的中位线，
∴$OE// AB$，$OE=\frac{1}{2}AB$。
∵点$F$、$G$在$AB$上，
∴$OE// FG$。
∵$OG// EF$，
∴四边形$OEFG$是平行四边形。
∵$EF\perp AB$，
∴$\angle EFG=90°$，
∴平行四边形$OEFG$是矩形。
(2)解：
∵$AD=10$，$E$是$AD$中点，
∴$AE=\frac{1}{2}AD=5$。
∵$EF\perp AB$，$EF=4$，
∴在$Rt\triangle AEF$中，$AF=\sqrt{AE^2-EF^2}=\sqrt{5^2-4^2}=3$。
∵四边形$OEFG$是矩形，
∴$FG=OE$，$OE=\frac{1}{2}AD=5$（$OE$为$Rt\triangle AOD$斜边中线），
∴$FG=5$。
∵$AB=AD=10$，
∴$AG=AF+FG=3+5=8$，
∴$BG=AB-AG=10-8=2$。
综上，$OE=5$，$BG=2$。