《2025年精练课堂分层作业九年级数学上册北师大版》

5. 如图,已知$\angle A = \angle D$,要使$\triangle ABC \backsim \triangle DEF$,还需添加一个条件,你添加的条件是∠B=∠DEF。(只需写一个条件,不添加辅助线和字母)

答案： ∠B=∠DEF

6. 如图,在$\triangle ABC$中,点$D在线段BC$上,$\angle B = \angle DAC$,$AC = 8$,$BC = 16$,那么$CD = $4。

答案： 4

7. 将一副三角尺按下图中的方法叠放在一起,则$\frac{BE}{EC}$的值是$\frac{\sqrt{3}-1}{2}$。

答案： 【解析】：设等腰直角三角尺的直角边AC=BC=1，含30°角的三角尺中，设CD=√3（因为tan60°=CD/AC=√3）。连接BD交AC于E，易证△AEB∽△CED（对顶角相等，内错角相等）。设EC=x，则AE=1-x，由相似比得AB/CD=AE/EC，即1/√3=(1-x)/x，解得x=√3/(1+√3)=(√3(√3-1))/2=(3-√3)/2，BE/EC=AE/EC=(1-x)/x=(1-(3-√3)/2)/((3-√3)/2)=(√3-1)/2。
【答案】：(√3 - 1)/2

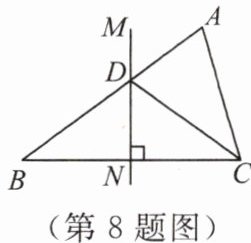
8. 如图,在$\triangle ABC$中,$BC的垂直平分线MN交AB于点D$,$CD平分\angle ACB$。若$AD = 2$,$BD = 3$,则$AC$的长为√10。

答案： √10

9. 如图,在$\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AD \perp BC$,垂足为$D$。求证：$AB^{2} = BD \cdot BC$。

答案： 证明：
∵∠BAC=90°，AD⊥BC，
∴∠ADB=∠BAC=90°。
∵∠B=∠B，
∴△ABD∽△CBA（两角分别相等的两个三角形相似）。
∴$\frac{AB}{BC} = \frac{BD}{AB}$。
∴$AB^{2} = BD \cdot BC$。

10. 如图,已知在矩形$ABCD$中,$E为AD上一点(AE ＞ DE)$,$BE \perp CE$。
(1) 求证：$\triangle EAB \backsim \triangle CDE$；
(2) 若$AB = 6$,$AD = 13$,求$AE$的长。

答案：
(1)
∵四边形ABCD是矩形，
∴∠A=∠D=90°，
∴∠ABE+∠AEB=90°．
∵BE⊥CE，
∴∠BEC=90°，又
∵∠AEB+∠BEC+∠DEC=180°，
∴∠AEB+∠DEC=90°，
∴∠ABE=∠DEC．
在△EAB和△CDE中，∠A=∠D=90°，∠ABE=∠DEC，
∴△EAB∽△CDE．
(2) 设AE=x，则DE=AD-AE=13-x．
∵△EAB∽△CDE，
∴AB/DE=AE/CD．
∵AB=CD=6，
∴6/(13-x)=x/6，即x(13-x)=36，整理得x²-13x+36=0．
解得x₁=9，x₂=4．
∵AE＞DE，
∴x＞13-x，即x＞6.5，
∴x=9．
∴AE的长为9．

1. 经过三边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”。如图,线段$CD是\triangle ABC$的“和谐分割线”,$\triangle ACD$为等腰三角形,$\triangle CBD和\triangle ABC$相似,$\angle A = 46^{\circ}$,则$\angle ACB$的度数为113°。

答案： 113°

2. 如图,在等边三角形$ABC$中,点$D$,$E分别在BC$,$AB$上,且$\angle ADE = 60^{\circ}$。
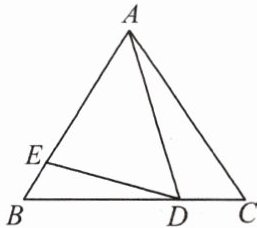
求证：$\triangle ADC \backsim \triangle DEB$。

答案： 证明：
∵△ABC是等边三角形，
∴∠B=∠C=60°，∠BAC=60°。
∵∠ADB+∠ADC=180°（平角定义），
且∠ADB=∠ADE+∠EDB（角的和差），∠ADE=60°，
∴∠ADB=60°+∠EDB，
∴∠ADC=180°-∠ADB=180°-(60°+∠EDB)=120°-∠EDB。
在△ADC中，∠ADC+∠DAC+∠C=180°（三角形内角和定理），
∵∠C=60°，
∴∠ADC=180°-∠C-∠DAC=120°-∠DAC。
∴120°-∠EDB=120°-∠DAC（等量代换），
∴∠EDB=∠DAC。
∵∠B=∠C=60°，∠EDB=∠DAC，
∴△ADC∽△DEB（两角对应相等的两个三角形相似）。