第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
1. 一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数字-1,2,-3,4.
(1) 摇匀后任意摸出1个球,摸出的乒乓球球面上的数字是负数的概率为
(2) 摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数字之和是正数的概率.
(1) 摇匀后任意摸出1个球,摸出的乒乓球球面上的数字是负数的概率为
$\frac{1}{2}$
;(2) 摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数字之和是正数的概率.
答案:
(1)
总共有4个乒乓球,标有数字$-1, 2, -3, 4$,其中负数有2个($-1$和$-3$)。
所以,摸出的乒乓球球面上的数字是负数的概率为:
$P = \frac{2}{4} = \frac{1}{2}$
(2)
首先,我们列出所有可能的摸球组合及其数字之和:
| 第一次摸球 | 第二次摸球 | 数字之和 |
|------------|------------|----------|
| -1 | 2 | 1 |
| -1 | -3 | -4 |
| -1 | 4 | 3 |
| 2 | -1 | 1 |
| 2 | -3 | -1 |
| 2 | 4 | 6 |
| -3 | -1 | -4 |
| -3 | 2 | -1 |
| -3 | 4 | 1 |
| 4 | -1 | 3 |
| 4 | 2 | 6 |
| 4 | -3 | 1 |
总共有12种等可能的结果,其中数字之和为正数的有8种。
所以,两次摸出的乒乓球球面上的数字之和是正数的概率为:
$P = \frac{8}{12} = \frac{2}{3}$
(1)
总共有4个乒乓球,标有数字$-1, 2, -3, 4$,其中负数有2个($-1$和$-3$)。
所以,摸出的乒乓球球面上的数字是负数的概率为:
$P = \frac{2}{4} = \frac{1}{2}$
(2)
首先,我们列出所有可能的摸球组合及其数字之和:
| 第一次摸球 | 第二次摸球 | 数字之和 |
|------------|------------|----------|
| -1 | 2 | 1 |
| -1 | -3 | -4 |
| -1 | 4 | 3 |
| 2 | -1 | 1 |
| 2 | -3 | -1 |
| 2 | 4 | 6 |
| -3 | -1 | -4 |
| -3 | 2 | -1 |
| -3 | 4 | 1 |
| 4 | -1 | 3 |
| 4 | 2 | 6 |
| 4 | -3 | 1 |
总共有12种等可能的结果,其中数字之和为正数的有8种。
所以,两次摸出的乒乓球球面上的数字之和是正数的概率为:
$P = \frac{8}{12} = \frac{2}{3}$
2. (2022·潍坊中考)从甲、乙两班各随机抽取10名同学(共20人)参加数学素养测试,将测试成绩分为如下的5组(满分为100分):
A组:50≤x<60,B组:60≤x<70,
C组:70≤x<80,D组:80≤x<90,
E组:90≤x≤100.
根据数据分别绘制频数分布直方图和扇形统计图如图.
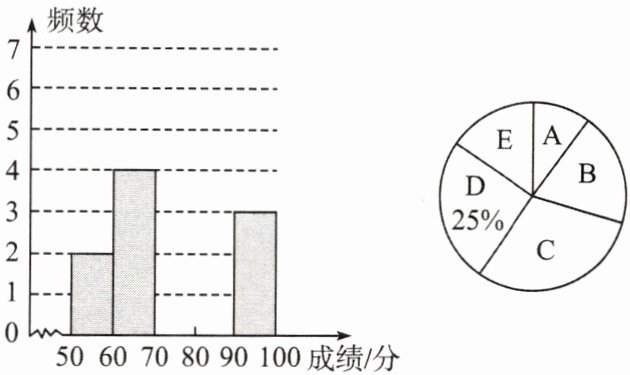
(1) 根据图中数据,补充完整频数分布直方图并估算参加测试的学生的平均成绩(取各组成绩的下限与上限的中间值近似地表示该组学生的平均成绩);
(2) 参加测试的学生被随机安排到4个不同的考场,其中小亮、小刚两名同学都参加测试,用树状图或列表法求小亮、小刚两名同学被分在不同考场的概率;
(3) 若甲、乙两班参加测试的学生成绩统计如下:
甲班:62,64,66,76,76,77,82,83,83,91;
乙班:51,52,69,70,71,71,88,89,99,100.
可计算得两班学生的样本平均成绩为$\overline{x}_{甲}= 76$,$\overline{x}_{乙}= 76$;样本方差为$s_{甲}^{2}= 80$,$s_{乙}^{2}= 275.4$.请用学过的统计知识评判甲、乙两班哪个班的数学素养总体水平较高,并说明理由.
A组:50≤x<60,B组:60≤x<70,
C组:70≤x<80,D组:80≤x<90,
E组:90≤x≤100.
根据数据分别绘制频数分布直方图和扇形统计图如图.

(1) 根据图中数据,补充完整频数分布直方图并估算参加测试的学生的平均成绩(取各组成绩的下限与上限的中间值近似地表示该组学生的平均成绩);
(2) 参加测试的学生被随机安排到4个不同的考场,其中小亮、小刚两名同学都参加测试,用树状图或列表法求小亮、小刚两名同学被分在不同考场的概率;
(3) 若甲、乙两班参加测试的学生成绩统计如下:
甲班:62,64,66,76,76,77,82,83,83,91;
乙班:51,52,69,70,71,71,88,89,99,100.
可计算得两班学生的样本平均成绩为$\overline{x}_{甲}= 76$,$\overline{x}_{乙}= 76$;样本方差为$s_{甲}^{2}= 80$,$s_{乙}^{2}= 275.4$.请用学过的统计知识评判甲、乙两班哪个班的数学素养总体水平较高,并说明理由.
答案:
(1) 总人数$20$人,D组$20× 25\%=5$人,C组$20 - 2 - 4 - 5 - 3 = 6$人。
频数分布直方图:A组$2$人,B组$4$人,C组$6$人,D组$5$人,E组$3$人。
平均成绩:$\frac{55×2 + 65×4 + 75×6 + 85×5 + 95×3}{20} = 76.5$(分)。
(2) 树状图:
开始
|
|--考场1--小亮--小刚(不同考场组合)
|
|--考场2--小亮--小刚
|
|--考场3--小亮--小刚
|
|--考场4--小亮--小刚
总共有$4×3 = 12$种等可能结果,分在不同考场有$12$种(小亮在考场$i$,小刚在考场$j$,$i\neq j$),概率为$\frac{12}{16}=\frac{3}{4}$。
(3)因为$\overline{x}_{甲}=\overline{x}_{乙}$,$s_{甲}^{2}<s_{乙}^{2}$,甲班成绩更稳定,所以甲班数学素养总体水平较高。
(1) 总人数$20$人,D组$20× 25\%=5$人,C组$20 - 2 - 4 - 5 - 3 = 6$人。
频数分布直方图:A组$2$人,B组$4$人,C组$6$人,D组$5$人,E组$3$人。
平均成绩:$\frac{55×2 + 65×4 + 75×6 + 85×5 + 95×3}{20} = 76.5$(分)。
(2) 树状图:
开始
|
|--考场1--小亮--小刚(不同考场组合)
|
|--考场2--小亮--小刚
|
|--考场3--小亮--小刚
|
|--考场4--小亮--小刚
总共有$4×3 = 12$种等可能结果,分在不同考场有$12$种(小亮在考场$i$,小刚在考场$j$,$i\neq j$),概率为$\frac{12}{16}=\frac{3}{4}$。
(3)因为$\overline{x}_{甲}=\overline{x}_{乙}$,$s_{甲}^{2}<s_{乙}^{2}$,甲班成绩更稳定,所以甲班数学素养总体水平较高。
查看更多完整答案,请扫码查看


