《2025年单元学习指导与练习八年级数学上册浙教版》

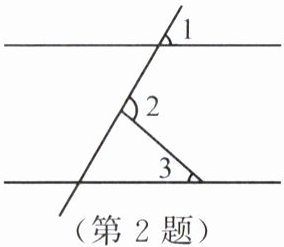
2. 如图所示，直线$a// b$，$\angle 1 = 60^{\circ}$，$\angle 2 = 100^{\circ}$，则$\angle 3$的度数为().

A.$30^{\circ}$
B.$40^{\circ}$
C.$50^{\circ}$
D.$80^{\circ}$

答案： B

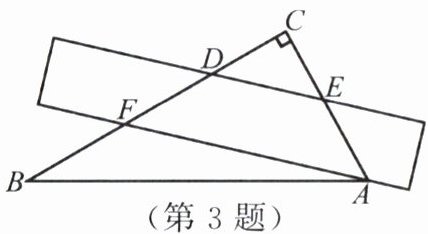
3. 将一把直尺和一把三角尺$ABC$(含$30^{\circ}$角)按如图所示的方式摆放.直尺的一边与三角尺的两直角边分别交于点$D$和点$E$，另一边与三角尺的两直角边分别交于点$F$和点$A$.如果$\angle CED = 50^{\circ}$，那么$\angle BFA$的度数为.

答案： 140

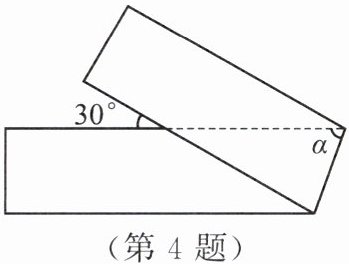
4. 有一条笔直的宽纸带，按如图所示的方式折叠，则$\angle \alpha$的度数为().

A.$50^{\circ}$
B.$60^{\circ}$
C.$75^{\circ}$
D.$85^{\circ}$

答案： C

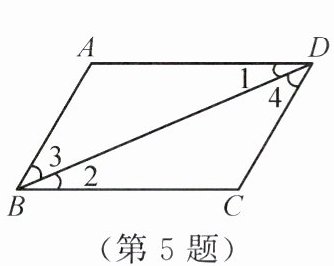
5. 如图所示，下列推理中，不正确的是().

A.$\because AB// CD$，$\therefore \angle ABC + \angle C = 180^{\circ}$
B.$\because \angle 1 = \angle 2$，$\therefore AD// BC$
C.$\because AD// BC$，$\therefore \angle 3 = \angle 4$
D.$\because \angle A + \angle ADC = 180^{\circ}$，$\therefore AB// CD$

答案： C

6. 请在横线上和括号内分别填写下列命题的证明过程和推理的依据.
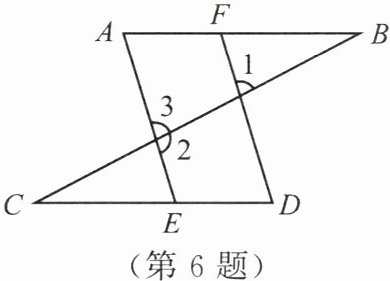
如图所示，已知$\angle 1$与$\angle 2$互补，$\angle A = \angle D$.求证：$AB// CD$.
证明：$\because \angle 1 + \angle 2 = 180^{\circ}$()，$\angle 2 + \angle 3 = 180^{\circ}$()，
$\therefore \angle 1 =$().
$\therefore$$//$().
$\therefore$$=$().
$\because \angle A = \angle D$()，
$\therefore$$=$(等量代换).
$\therefore AB// CD$().

答案： 证明：
$\because \angle 1 + \angle 2 = 180^{\circ}$(已知)，$\angle 2 + \angle 3 = 180^{\circ}$(平角的定义)，
$\therefore \angle 1 =\angle3$(同角的补角相等)。
$\therefore CE// AF$(同位角相等，两直线平行)。
$\therefore \angle A=\angle CEA$(两直线平行，内错角相等)。
$\because \angle A = \angle D$(已知)，
$\therefore \angle CEA=\angle D$(等量代换)。
$\therefore AB // CD$(同位角相等，两直线平行)。
故答案为：已知；平角的定义；$\angle 3$；同角的补角相等；$CE$；$AF$；同位角相等，两直线平行；$\angle A$；$\angle CEA$；两直线平行，内错角相等；已知；$\angle CEA$；$\angle D$；同位角相等，两直线平行。