《2025年单元学习指导与练习八年级数学上册浙教版》

10. 如图所示，点$P$的坐标为$(4,3)$，把点$P$绕坐标原点$O$按逆时针方向旋转$90^{\circ}$后得到点$Q$.
(1) 写出点$Q$的坐标：.
(2) 若把点$Q$向右平移$m$个单位长度，向下平移$2m$个单位长度后，得到的点$Q'$恰好落在第三象限，求$m$的取值范围.

]

答案：
(1) 点 $Q$ 的坐标为 $(-3, 4)$。
(2)
由题意，点$Q$的坐标为$(-3,4)$，把点$Q$ 向右平移 $m$ 个单位长度，向下平移 $2m$ 个单位长度后，得到的点$Q^{\prime}$的坐标为$(-3+m,4-2m)$，
因为点$Q^{\prime}$落在第三象限内，
所以$\begin{cases}-3+m ＜0, \\4-2m ＜0.\end{cases}$
解得$2 ＜m ＜3$。

11. 如图所示，$\triangle ABC$在平面直角坐标系中，$A$，$B$，$C$三点的坐标分别是$A(-3,3)$，$B(-5,-1)$，$C(-1,1)$. 平移$\triangle ABC$，使点$A$，$B$，$C$的对应点分别是$A'(1,1)$，$B'$，$C'$.
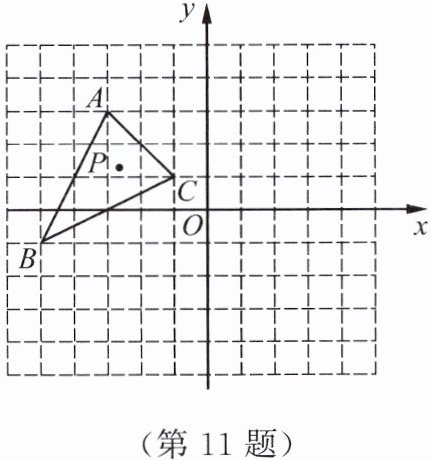
(1) 请画出平移后的$\triangle A'B'C'$.
(2) 求出四边形$CBB'A'$的面积.
(3) 若$P$是$\triangle ABC$内部的一点，平移$\triangle ABC$，点$P$的对应点是$P'(m,n)$. 若$\triangle CBA'$与$\triangle CP'A'$的面积相等，求$m + n$的取值范围.

]

答案：
(1) 由A(-3,3)平移至A'(1,1)，平移向量为(4,-2)。则B'(-5+4,-1-2)=(-1,-3)，C'(-1+4,1-2)=(3,-1)。画出△A'B'C'（图略）。
(2) 四边形CBB'A'顶点坐标：C(-1,1)，B(-5,-1)，B'(-1,-3)，A'(1,1)。利用鞋带公式：
$\begin{aligned}S&=\frac{1}{2}\vert(-1)(-1)+(-5)(-3)+(-1)(1)+1(1)-[1(-5)+(-1)(-1)+(-3)(1)+1(-1)]\vert\\&=\frac{1}{2}\vert1+15-1+1-[-5+1-3-1]\vert\\&=\frac{1}{2}\vert16 - (-8)\vert=12\end{aligned}$
(3) △CBA'与△CP'A'公共底边A'C（y=1，长2），面积相等则高相等。B(-5,-1)到y=1距离为2，故P'(m,n)到y=1距离为2，得n=-1（n=3舍去，P'不在△A'B'C'内）。P(m-4,1)在△ABC内部，△ABC中y=1线段横坐标范围(-4,-1)，则-4＜m-4＜-1，即0＜m＜3。m+n=m-1，故-1＜m+n＜2。
(1) 图略；
(2) 12；
(3) (-1,2)