第67页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
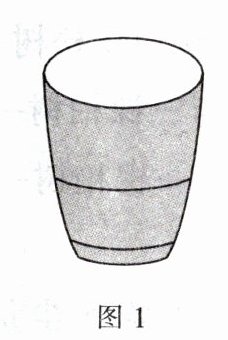
6. (2024·北京) 小云有一个圆柱形水杯(记为 1 号杯)。在科技活动中,小云用所学数学知识和人工智能软件设计了一个新水杯,并将其制作出来。新水杯(记为 2 号杯)的示意图如图所示。当 1 号杯和 2 号杯中都有 $V$ $mL$ 水时,小云分别记录了 1 号杯的水面高度 $h_1$($cm$)和 2 号杯的水面高度 $h_2$($cm$),部分数据如下:
| $V/mL$ | $0$ | $40$ | $100$ | $200$ | $300$ | $400$ | $500$ |
| $h_1/cm$ | $0$ | | $2.5$ | $5.0$ | $7.5$ | $10.0$ | $12.5$ |
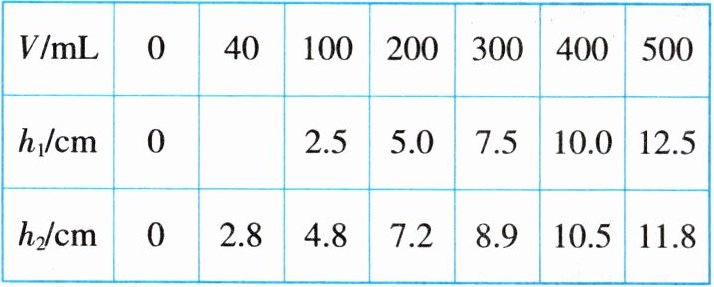
| $h_2/cm$ | $0$ | $2.8$ | $4.8$ | $7.2$ | $8.9$ | $10.5$ | $11.8$ |
(1) 补全表格(结果保留小数点后一位)。
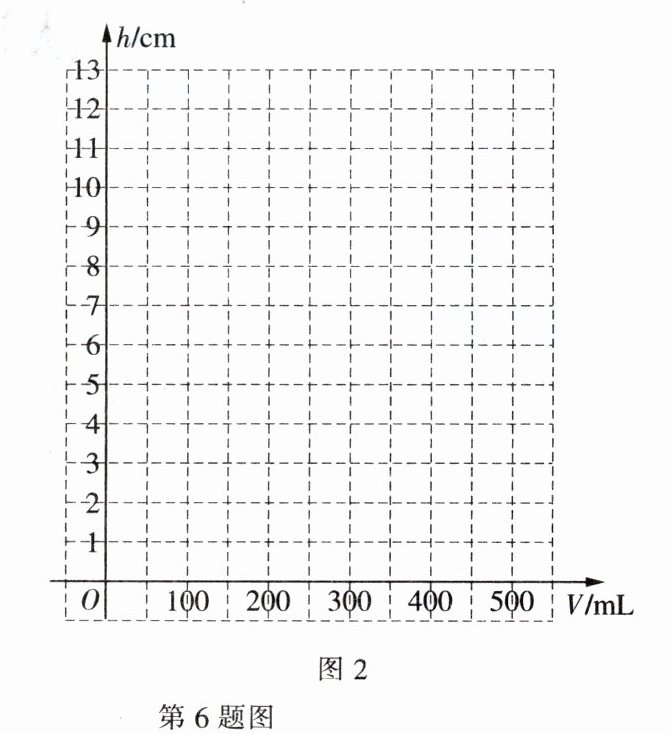
(2) 通过分析数据,发现可以用函数刻画 $h_1$ 与 $V$,$h_2$ 与 $V$ 之间的关系。在平面直角坐标系中,画出这两个函数的图象。
(3) 根据以上数据与函数图象,回答下列问题:
①当 1 号杯和 2 号杯中都有 $320$ $mL$ 水时,2 号杯的水面高度与 1 号杯的水面高度的差约为______(结果保留小数点后一位)$cm$;
②在①的条件下,将 2 号杯中的一部分水倒入 1 号杯中,当两个水杯的水面高度相同时,其水面高度约为______(结果保留小数点后一位)$cm$。
| $V/mL$ | $0$ | $40$ | $100$ | $200$ | $300$ | $400$ | $500$ |
| $h_1/cm$ | $0$ | | $2.5$ | $5.0$ | $7.5$ | $10.0$ | $12.5$ |



| $h_2/cm$ | $0$ | $2.8$ | $4.8$ | $7.2$ | $8.9$ | $10.5$ | $11.8$ |
(1) 补全表格(结果保留小数点后一位)。
(2) 通过分析数据,发现可以用函数刻画 $h_1$ 与 $V$,$h_2$ 与 $V$ 之间的关系。在平面直角坐标系中,画出这两个函数的图象。
(3) 根据以上数据与函数图象,回答下列问题:
①当 1 号杯和 2 号杯中都有 $320$ $mL$ 水时,2 号杯的水面高度与 1 号杯的水面高度的差约为______(结果保留小数点后一位)$cm$;
②在①的条件下,将 2 号杯中的一部分水倒入 1 号杯中,当两个水杯的水面高度相同时,其水面高度约为______(结果保留小数点后一位)$cm$。
答案:
6. (1)1.0 (2)图象略。(3)①1.2 ②8.6
查看更多完整答案,请扫码查看


