《2025年新课程能力培养八年级数学上册北师大版》

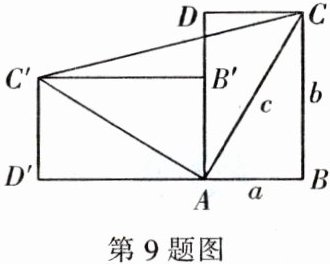
9. 一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法。如图,火柴盒的一个侧面 $ABCD$ 倒下到 $AB'C'D'$ 的位置,连接 $CC'$,设 $AB = a$,$BC = b$,$AC = c$,请利用四边形 $BCC'D'$ 的面积验证勾股定理：$a^2 + b^2 = c^2$。

答案： 解：
∵Rt△A'C'D'≌Rt△CAB，
∴CA'=AC=c，AD'=CB=b，C'D'=AB=a，∠AC'D'=∠CAB。
∵∠AC'D'+∠D'A'C=90°，
∴∠BAC+∠D'A'C=90°。
∴∠C'A'C=180°-90°=90°。
∴△C'A'C是一个等腰直角三角形，它的面积等于$\frac{1}{2}c^{2}$。又
∵四边形BCC'D'是一个直角梯形，
∴$\frac{1}{2}(a+b)^{2}=2×\frac{1}{2}ab+\frac{1}{2}c^{2}$，
∴$a^{2}+b^{2}=c^{2}$。

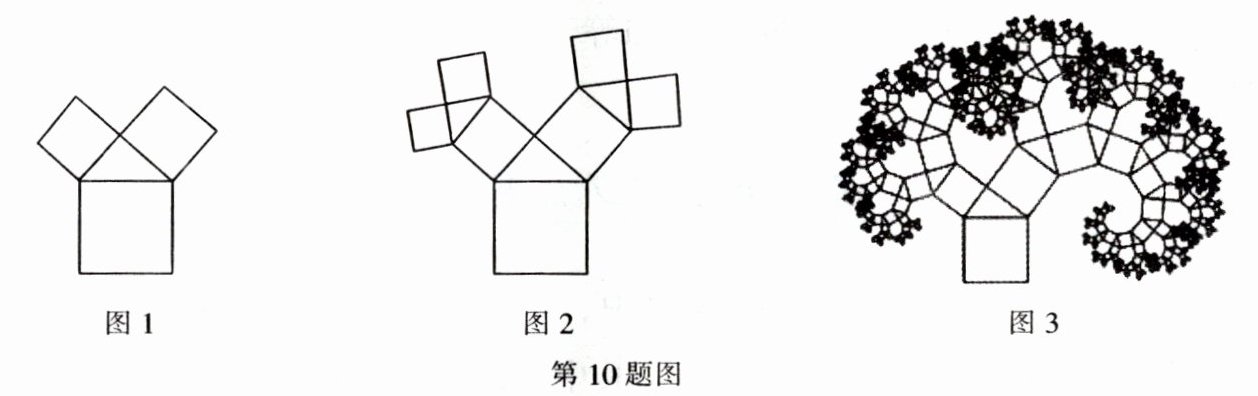
10. (2024·大庆) 如图 1,直角三角形的两个锐角分别是 $40°$ 和 $50°$,其三边上分别有一个正方形。执行下面的操作：由两个小正方形向外分别作锐角为 $40°$ 和 $50°$ 的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形。图 2 是 1 次操作后的图形,图 3 是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”。若图 1 中的直角三角形斜边长为 $2$,则 10 次操作后图形中所有正方形的面积和为 $\underline{\quad\quad}$。

答案： 48

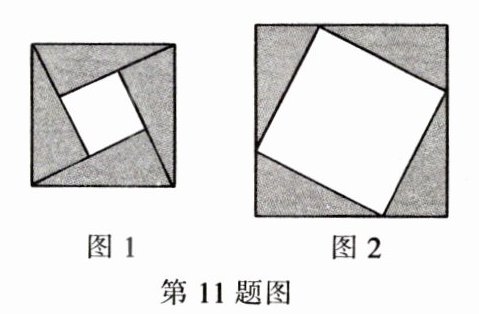
11. (2024·眉山) 如图,图 1 是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成。若图 1 中大正方形的面积为 $24$,小正方形的面积为 $4$,现将这四个直角三角形拼成图 2,则图 2 中大正方形的面积为( )

A.$24$
B.$36$
C.$40$
D.$44$

答案： D

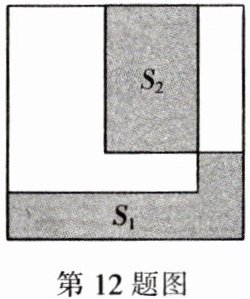
12. (2023·日照) 已知直角三角形的三边 $a$,$b$,$c$ 满足 $c ＞ a ＞ b$,分别以 $a$,$b$,$c$ 为边作三个正方形,把两个较小的正方形放置在最大正方形内,如图,设三个正方形无重叠部分的面积为 $S_1$,均重叠部分的面积为 $S_2$,则( )

A.$S_1 ＞ S_2$
B.$S_1 ＜ S_2$
C.$S_1 = S_2$
D.$S_1$,$S_2$ 大小无法确定

答案： C