《2025年新课程能力培养八年级数学上册北师大版》

8. 经验表明,树在一定的成长阶段,其树高y(m)可以近似地看成胸径x(m)的一次函数。已知测得某种树胸径为0.2m时,树高为20m；胸径为0.6m时,树高为30m。
(1)求树高y(m)与其胸径x(m)之间的关系式。
(2)当这种树的胸径为0.5m时,其树高是多少？
(3)若这种树的胸径增长0.28m,其树高应增长多少米？

答案： 解：（1）设y与x之间的关系式为y=kx+b。由一次函数的性质，当自变量x每增加1时，函数值的变化量“均匀”地增加k。又
∵胸径为0.2 m时，树高为20 m；胸径为0.6 m时，树高为30 m，
∴k=(30-20)÷(0.6-0.2)=25。
∴y=25x+b。将x=0.2，y=20代入，得25×0.2+b=20，
∴b=15。
∴树高y与其胸径x之间的关系式为y=25x+15。（2）当x=0.5时，y=25×0.5+15=27.5。
∴树高为27.5 m。（3）依题意，得y₁=25(x+0.28)+15=25x+15+7，则y₁-y=25x+15+7-(25x+15)=7。
∴当这种树的胸径增长0.28 m时，其树高增长7 m。

9. 某加油站推出促销活动,一张加油卡的面值是1000元,打九折出售。使用这张加油卡加油,每升油的价格降低0.30元。假设这张加油卡的面值能够一次性全部用完。
(1)购买一张加油卡实际花了多少钱？
(2)减价后油的价格为y元/L,原价为x元/升,求y关于x的函数表达式。
(3)油的原价是7.30元/L,优惠后每升油的价格比原价便宜多少元？

答案： 解：（1）由题意，知1000×0.9=900（元）。答：购买一张加油卡实际花了900元。（2）由题意知，y=0.9·(x-0.3)=0.9x-0.27，
∴y关于x的函数表达式为y=0.9x-0.27。（3）当x=7.3时，y=0.9×7.3-0.27=6.3。
∴7.3-6.3=1。
∴优惠后每升油的价格比原价便宜1元。

10. (2024·西藏)将正比例函数y= 2x的图象向上平移3个单位长度后,得到的函数图象的表达式为____。

答案： y=2x+3

11. (2024·凉山州)如图,一次函数y= kx+b的图象经过A(3,6),B(0,3)两点,交x轴于点C,则△AOC的面积为____。

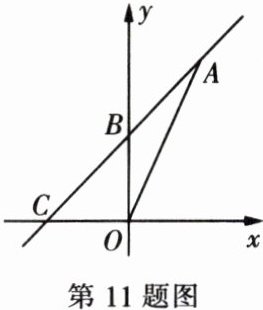
答案： 9

12. (2024·上海)某种商品的销售额y(万元)与广告投入x(万元)成一次函数关系,当投入10万元时销售额为1000万元,当投入90万元时销售额为5000万元,则投入80万元时,销售额为____万元。

答案： 4500

13. (2024·陕西)实验表明,在某地,温度在15℃至25℃的范围内,一种蟋蟀1min的平均鸣叫次数y可近似看成该地当时温度x(℃)的一次函数。已知这种蟋蟀在温度为16℃时,1min平均鸣叫92次；在温度为23℃时,1min平均鸣叫155次。
(1)求y与x之间的关系式。
(2)当这种蟋蟀1min平均鸣叫128次时,该地当时的温度约是多少？

答案： 解：（1）设y与x之间的关系式为y=kx+b（k，b为常数，且k≠0），由一次函数的性质，当自变量x每增加1，函数值y的变化量“均匀”地增加k。
∵蟋蟀在温度为16 ℃时，1 min平均鸣叫92次；在温度为23 ℃时，1 min平均鸣叫155次，
∴k=(155-92)÷(23-16)=9。
∴y=9x+b。将x=16，y=92代入y=9x+b，得b=-52。
∴y与x之间的关系式为y=9x-52。（2）将y=128代入y=9x-52，得9x-52=128。解得x=20。答：该地当时的温度约是20 ℃。