《2025年新课程能力培养八年级数学上册北师大版》

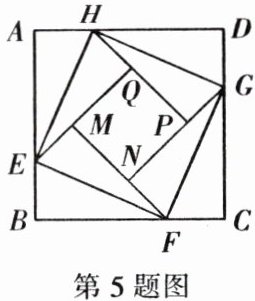
5. 如图是由“赵爽弦图”变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形 $ABCD$、正方形 $EFGH$、正方形 $MNPQ$ 的面积分别为 $S_1$,$S_2$,$S_3$。若 $S_1 + S_2 + S_3 = 60$,则 $S_2$ 的值是( )


A.$12$
B.$15$
C.$20$
D.$30$

答案： C

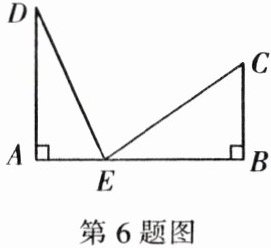
6. 如图,铁路上 $A$,$B$ 两点相距 $25$ km,$C$,$D$ 为两村庄,$DA \perp AB$ 于点 $A$,$CB \perp AB$ 于点 $B$,已知 $DA = 15$ km,$CB = 10$ km,现在要在铁路 $AB$ 上建一个土特产收购站 $E$,使得 $C$,$D$ 两村到 $E$ 站的距离相等,那么 $E$ 站应建在离 $A$ 点多远处？

答案： 解：设AE=x km，则$x^{2}+15^{2}=10^{2}+(25-x)^{2}$，解得x=10 km，即E站应建在离A点10 km处。

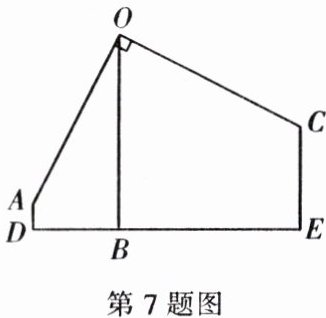
7. 如图是高空秋千的示意图,小李从起始位置点 $A$ 处绕着点 $O$ 经过最低点 $B$,最终荡到最高点 $C$ 处。若 $\angle AOC = 90°$,点 $A$ 与点 $B$ 的高度差 $AD = 1$ m,水平距离 $BD = 4$ m。求点 $C$ 与点 $B$ 的高度差 $CE$。

答案：
解：如图，作AF⊥BO于点F，CG⊥BO于点G，
∵AD⊥DB，OB⊥DE，
∴∠ADB=∠DBO=∠OBE=90°。
∴AD//OB。
∴∠AFO=∠DAF=90°。
∴∠ADB=∠DBF=∠AFB=∠DAF=90°。
∴四边形ADBF为长方形。同理，四边形BECG为长方形。
∵∠AOC=∠AOF+∠COG=90°，∠AOF+∠OAF=90°，
∴∠COG=∠OAF。
∵∠CGO=∠AFO=90°，AO=CO，
∴△AOF≌△OCG（AAS）。
∴OG=AF=BD=4 m。设AO=x m，在Rt△AFO中，$AF^{2}+OF^{2}=AO^{2}$，即$4^{2}+(x-1)^{2}=x^{2}$，解得x=8.5。则CE=GB=OB-OG=8.5-4=4.5（m）。

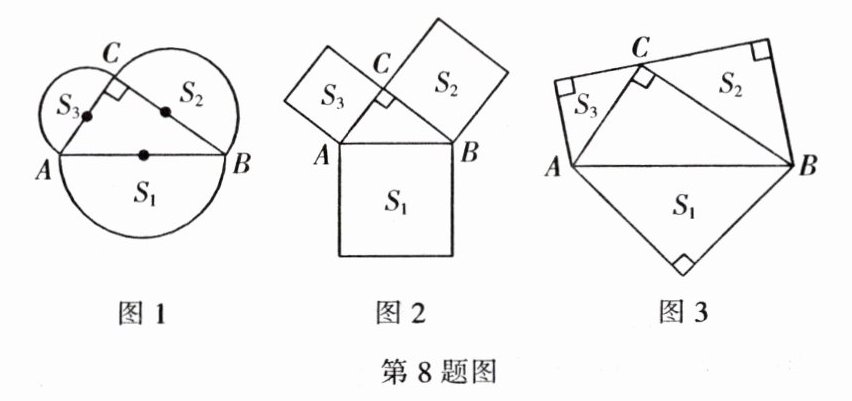
8. 如图 1,分别以 $Rt\triangle ABC$ 的三条边为直径向外作三个半圆,其面积分别用 $S_1$,$S_2$,$S_3$ 表示,则 $S_1 = S_2 + S_3$。
(1) 如图 2,分别以 $Rt\triangle ABC$ 的三条边为边长向外作三个正方形,其面积分别用 $S_1$,$S_2$,$S_3$ 表示,那么 $S_1$,$S_2$,$S_3$ 之间有什么关系？请说明理由。
(2) 如图 3,分别以 $Rt\triangle ABC$ 的三条边为边长向外作三个等腰直角三角形,其面积分别用 $S_1$,$S_2$,$S_3$ 表示,那么 $S_1$,$S_2$,$S_3$ 之间有什么关系？请说明理由。

答案： 解：（1）$S_{1}=S_{2}+S_{3}$。理由：设Rt△ABC的三边BC，AC，AB的长分别为a，b，c，由勾股定理得$c^{2}=a^{2}+b^{2}$。又
∵$S_{1}=c^{2}$，$S_{2}=a^{2}$，$S_{3}=b^{2}$，
∴$S_{1}=S_{2}+S_{3}$。（2）$S_{1}=S_{2}+S_{3}$。理由：
∵$S_{1}=\frac{1}{4}c^{2}$，$S_{2}=\frac{1}{4}a^{2}$，$S_{3}=\frac{1}{4}b^{2}$，
∴$S_{2}+S_{3}=\frac{1}{4}a^{2}+\frac{1}{4}b^{2}=\frac{1}{4}(a^{2}+b^{2})=\frac{1}{4}c^{2}=S_{1}$。