《2025年新课程能力培养八年级数学上册北师大版》

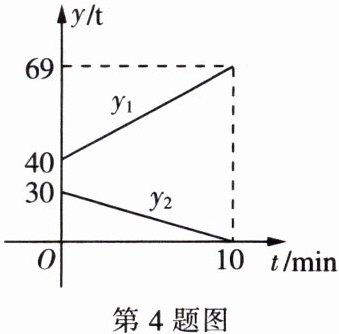
4. 空军某部的加油机接到命令,要求立即给另一架正在飞行的运输机进行空中加油。在加油过程中,设运输机的油箱余油量为 $y_1$ $t$,加油机的加油油箱余油量为 $y_2$ $t$,加油时间为 $t$ $min$,$y_1$,$y_2$ 与 $t$ 之间的函数图象如图所示,结合图象回答下列问题：
(1) 加油机的加油油箱中装载了多少吨油？将这些油全部加给运输机需要多少分钟？
(2) 求加油过程中,运输机的余油量 $y_1$($t$)与时间 $t$($min$)之间的关系式,所求的关系式中 $k$ 和 $b$ 的实际意义是什么？
(3) 运输机加完油后,以原速继续飞行,需 $10$ $h$ 到达目的地,油量是否够用？请说明理由。

答案： 4. 解：（1）由图象知，加油机的加油油箱中装载了 30 t 油，全部加给运输机需要 10 min。（2）设 y₁=kt+b，由图象知 b=40，
∵y₁=kt+40 的图象经过点（10，69），
∴10k+40=69。解得 k=2.9。
∴所求函数的表达式为 y₁=2.9t+40（0≤t≤10），所求的表达式中 k 的实际意义就是每分钟运输机的油箱所增加的油量是 2.9 t，b 的实际意义就是运输机在加油之前油箱中的剩余油量是 40 t。（3）由图象知，运输机 10 min 耗油 1 t，
∴运输机的耗油量为每分钟 0.1 t，
∴10 h 耗油量为 10×60×0.1=60（t）＜69（t），
∴油量够用。

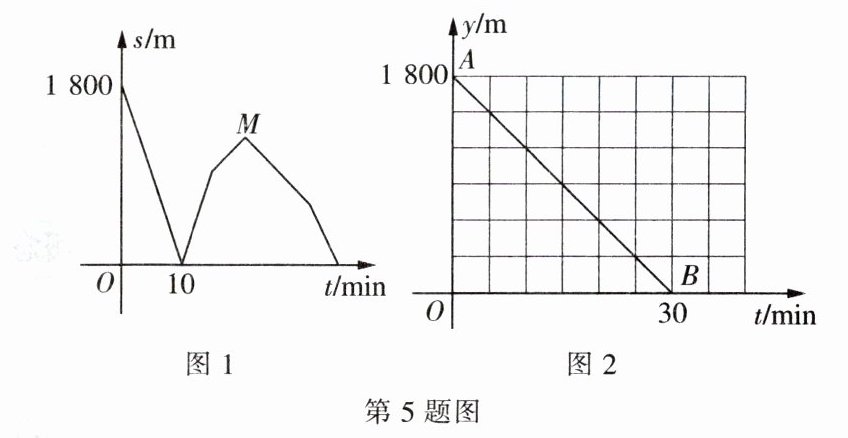
5. 小李从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小李到达商店比妈妈返回商店早 $5$ $min$,在此过程中,设妈妈从商店出发开始所用时间为 $t$($min$),图 1 表示两人之间的距离 $s$($m$)与时间 $t$($min$)的函数关系的图象；图 2 中线段 $AB$ 表示小李和商店的距离 $y_1$($m$)与时间 $t$($min$)的函数关系的图象的一部分。请根据所给信息解答下列问题：
(1) 填空：妈妈骑车的速度是______ $m/min$,妈妈在家装载货物所用时间是______ $min$,点 $M$ 的坐标是______。
(2) 直接写出妈妈和商店的距离 $y_2$($m$)与时间 $t$($min$)之间的关系式,并在图 2 中画出其函数图象。
(3) 小李到达商店之前,出发多长时间时两人相距 $360$ $m$？

答案： 5. （1）120 5 提示：由题图 2 知小李从家到商店的时间为 30 min，
∴小李的速度为 60 m/min，妈妈从出发到返回店里所用时间为 35 min。由题图 1 可知妈妈的速度为（1800-10×60）÷60=120（m/min），
∴妈妈往返所用时间为 3600/120=30（min），
∴妈妈在家装载货物所用时间为 5 min。（20，1200）（2）y₂={120t (0≤t＜15), 1800 (15≤t＜20), -120t+4200 (20≤t≤35)。图象略。（3）由题意可知，小李的速度为 60 m/min，妈妈的速度为 120 m/min。①相遇前，依题意有 60t+120t+360=1800。解得 t=8。②相遇后，依题意有 60t+120t-360=1800。解得 t=12。
∴小李到达商店之前，出发 8 min 或 12 min 时两人相距 360 m。