《2025年新课程能力培养八年级数学上册北师大版》

5. 已知实数：$ -\dfrac{11}{12} $,$ 0.3 $,$ \pi $,$ 0 $,$ -5 $,$ 0.728 $,$ 3.14 $,$ 0.3030030003… $(每相邻两个 $ 3 $ 之间 $ 0 $ 的个数逐次增加 $ 1 $)。请你根据下面要求解答问题：
有理数集合：…$\{ \}$；
无理数集合：…$\{ \}$；
负实数集合：…$\{ \}$；
实数由小到大排列：______。

答案： 解：（1）有理数集合：$\{-\dfrac{11}{12},0.3,0,-5,0.728,3.14\cdots\}$ （2）无理数集合：$\{π,0.303\ 003\ 000\ 3\cdots$（每相邻两个3之间0的个数逐次增加1）…$\}$ （3）负实数集合：$\{-\dfrac{11}{12},-5\cdots\}$（4）实数由小到大排列：$-5$，$-\dfrac{11}{12}$，0，0.3，0.303 003 000 3…（每相邻两个3之间0的个数逐次增加1），0.728，3.14，$π\cdots$

6. 请在 $ 5 × 5 $ 的正方形网格中作出满足下列条件的直角三角形。
(1) 三条边的长都是有理数。
(2) 两条边的长是有理数,另一条边的长是无理数。
(3) 一条边的长是有理数,另两条边的长是无理数。
(4) 三条边的长都是无理数。

答案：
(1) 取顶点坐标(0,0)，(3,0)，(3,4)。直角边分别为3和4，斜边为5，均为有理数。
(2) 取顶点坐标(0,0)，(1,0)，(1,1)。直角边为1和1（有理数），斜边为√2（无理数）。
(3) 取顶点坐标(0,0)，(2,0)，(1,1)。斜边为2（有理数），直角边均为√2（无理数）。
(4) 取顶点坐标(0,0)，(2,2)，(1,3)。三边分别为√2，2√2，√10，均为无理数。

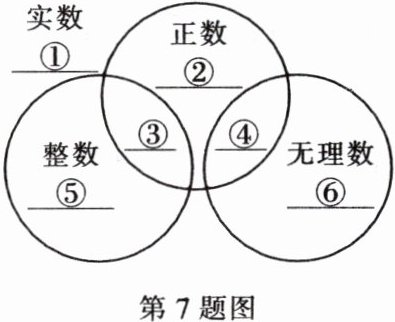
7. 聪聪在学完实数后,对实数进行分类时,发现实数、整数、正数和无理数有如图所示的关系,请你分别写出图中横线上序号所对应的数。(各写出一个数即可)

①______；
②______；
③______；
④______；
⑤______；
⑥______。

答案： 解：①$-\dfrac{1}{2}$②$\dfrac{1}{2}$ ③3 ④2.024 002 400 024…（每相邻两个24之间0的个数逐次增加1） ⑤$-7$ ⑥$π$

8. 在数轴上作出满足下列条件的实数 $ x $ 所对应的点：
(1) 一个负实数 $ x^{2}= 2 $；
(2) 实数 $ x^{2}= 10 $。

答案：
(1) 解：
∵$x^2 = 2$且$x$为负实数，
∴$x=-\sqrt{2}$。
作图步骤：①在数轴上，以原点$O$为直角顶点，作两直角边均为1个单位长度的直角三角形，斜边长度为$\sqrt{1^2+1^2}=\sqrt{2}$；②以$O$为圆心，斜边为半径画弧，交数轴负半轴于点$A$，则点$A$即为所求。
(2) 解：
∵$x^2 = 10$，
∴$x=\pm\sqrt{10}$。
作图步骤：①在数轴上，以原点$O$为起点，在正半轴取3个单位长度得点$B(3,0)$，过$B$作数轴垂线，截取$BC=1$个单位长度；②连接$OC$，则$OC=\sqrt{3^2+1^2}=\sqrt{10}$；③以$O$为圆心，$OC$长为半径画弧，交数轴正半轴于点$D$，负半轴于点$E$，则点$D$、$E$即为所求。