《2025年新课程能力培养八年级数学上册北师大版》

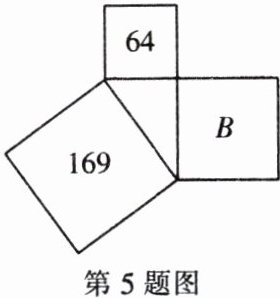
5. 如图,以直角三角形的三条边为边长分别作正方形,依据图中所给条件,回答下列问题：
(1)正方形B的面积是多少？
(2)设正方形B的边长为$b$,则$b$满足什么条件？$b$是有理数吗？
(3)估计$b$的值(结果精确到0.1),并用计算器验证你的估计。

答案： （1）105。 （2）$b^{2}=105$，不是。 （3）10.2，验证略。

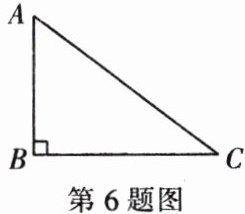
6. 如图,在$\triangle ABC$中,$\angle ABC = 90^{\circ}$,$AB = 3$,$AC = 4$。
(1)$\triangle ABC$的边BC的长是整数吗？如果不是整数,那么它的整数部分是多少？请说明理由。
(2)请你借助计算器仿照教材中求面积为2的正方形边长的方法,估计BC边的长大约是多少。(精确到0.0001)

答案： 解：（1）$BC$的长不是整数，$BC$边的长的整数部分是2。理由：在$\triangle ABC$中，$\angle ABC=90^{\circ}$，$AB=3$，$AC=4$，由勾股定理，可得$BC^{2}=AC^{2}-AB^{2}=16-9=7$。
∵$4＜$$BC^{2}＜9$，
∴$2＜BC＜3$。
∴$BC$的长不是整数，$BC$边的长的整数部分是2。（2）用无限逼近的方法可得$BC\approx$$2.64575$。（无限逼近的过程略）

7. 《清秘藏》是明代所著的工艺美术鉴赏著作,其中所述的刺绣在中国经过长时间的发展,已经形成了极高的工艺水平和独特的工艺门类。现有一张长方形绣布,长、宽之比为$4:3$,面积为$588cm^{2}$。
(1)这块绣布的长和宽是有理数吗？如果是有理数,请求出它的周长；如果不是,请说明理由。
(2)刺绣师傅想利用这张绣布裁出一张面积为$340cm^{2}$的完整圆形绣布用来绣花鸟图,她能够裁出来吗？如果能够裁出来,那么这个完整的圆形绣布的半径是有理数吗？请说明理由。

答案： 解：（1）是有理数。设绣布的长为$4x\ cm$，宽为$3x\ cm$，根据题意，得$4x\cdot 3x=588$，即$12x^{2}=588$。
∴$x^{2}=49$。
∵$x＞0$，
∴$x=7$。$4x=28$，$3x=21$。
∴绣布的长为$28\ cm$，宽为$21\ cm$。
∴这块绣布的长和宽都是有理数。
∴$2×(28+21)=98\ (cm)$。答：这块绣布的周长为$98\ cm$。（2）能够裁出来完整的圆形绣布。理由：设完整的圆形绣布的半径为$r\ cm$，根据题意，得$\pi r^{2}=340$。
∴$r^{2}=\frac{340}{\pi}\approx108.225$。
∵$100＜r^{2}＜$$121$，
∴$10＜r＜11$。
∵$108.16＜r^{2}＜110.25$，
∴$10.4＜r＜10.5$。
∴$2r＜21$，
∴能够裁出来完整的圆形绣布。
∵$\pi$是无限不循环小数，
∴$r^{2}=340÷\pi=108.22536\cdots$一定是无限不循环小数。
∴$r$不是分数，也不是整数，
∴$r$不是有理数。

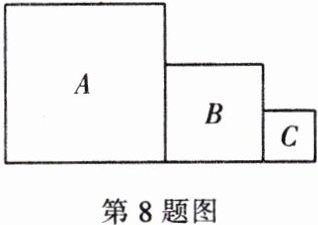
8. (2024·深圳)如图,A,B,C均为正方形,若A的面积为10,C的面积为1,则B的边长可以是______(写出一个即可)。

答案： 2（答案不唯一）

9. (2024·广东)完全相同的4个正方形面积之和是100,则正方形的边长是( )

A.2
B.5
C.10
D.20

答案： B