《2025年新课程能力培养八年级数学上册北师大版》

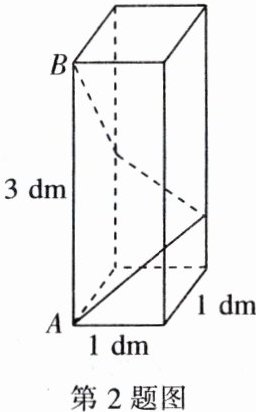
2. 如图是一个高为$3dm$,底面是边长为$1dm$的正方形的长方体包装盒。如果用一根麻绳从点$A开始经过4个侧面绕一圈到达点B$,请计算所用麻绳的最短长度。

答案：
2. 解：如图，将长方体包装盒侧面沿棱AB展开，得到如图所示的长方形AA₁B₁B，连接AB₁，由两点之间线段最短，AB₁长就是所用麻绳的最短长度。在Rt△AA₁B₁中，AA₁=4×1=4（dm），A₁B₁=3 dm。由勾股定理，得AB₁²=AA₁²+A₁B₁²=4²+3²=25。
∴AB₁=5 dm。答：所用麻绳的最短长度为5 dm。

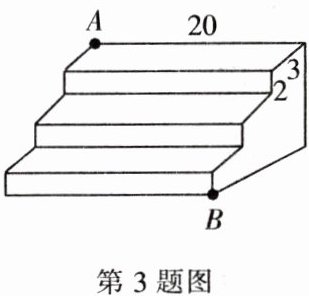
3. 如图,三级台阶的每一级的长、宽、高分别为$20dm$,$3dm$,$2dm$,点$A和点B$分别是台阶两个相对的端点。点$A$处有一只蚂蚁,想到点$B$处去吃可口的食物,求蚂蚁爬行的最短路程。

答案：
3. 解：如图，三级台阶平面展开图为长方形，则BC=20 dm，AC=(2+3)×3=15（dm），则蚂蚁沿台阶面爬行到点B处的最短路程是该长方形对角线AB的长。在Rt△ACB中，由勾股定理，得AB²=AC²+BC²=20²+15²=25²。
∴AB=25 dm。答：蚂蚁沿着台阶面爬到点B处的最短路程是25 dm。

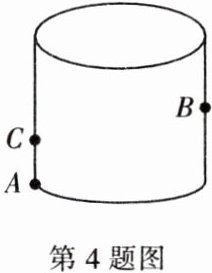
4. 如图,这是一个高为$10cm$、底面圆周长为$32cm$、没有上盖的圆柱形食品盒。一只蚂蚁在盒外表面距下底面$3cm的点C$处,想吃到盒内表面对侧中点$B$处的食物,那么蚂蚁需要爬行的最短路程是多少？

答案： 4. 解：
∵圆柱形食品盒高10 cm、底面圆周长为32 cm，且蚂蚁从盒外表面距下底面3 cm的C处，爬行到盒内表面对侧中点B处，
∴相当于蚂蚁从一个高为(7+5)cm、底面圆周长为32 cm的圆柱形食品盒的下底面上的点C处，爬行到对侧上底面上的点B处。将转化得到的圆柱体侧面展开，得到一个长为32 cm、宽为12 cm的长方形，则这长方形一半，即长为16 cm、宽为12 cm的长方形的对角线就是蚂蚁吃到食物需要爬行的最短路程。由勾股定理，得16²+12²=400=20²，
∴蚂蚁吃到食物需要爬行的最短路程为20 cm。

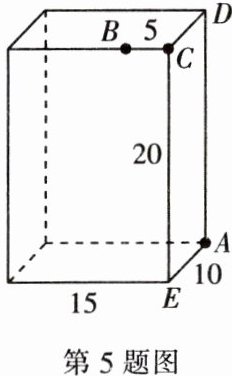
5. 如图,长方体的长为$15$,宽为$10$,高为$20$,点$B与点C的距离为5$。一只蚂蚁要沿着长方体的表面从点$A爬行到点B$,问蚂蚁爬行的路线有多少种？请通过计算说明哪一种路线最短。

答案：
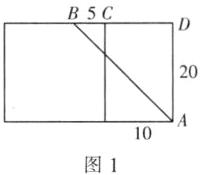
5. 解：蚂蚁爬行的路线有3种。①当蚂蚁爬行经过长方体的右侧表面与前面这两个侧面时，我们将这两个侧面展开所得到的平面图形如图1所示。
∵长方体的宽为10，高为20，点B离点C的距离是5，
∴BD=CD+BC=10+5=15，AD=20。在Rt△ABD中，由勾股定理，可得AB²=BD²+AD²=15²+20²=625。

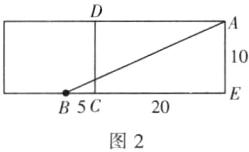
②当蚂蚁爬行经过长方体的右侧表面与上底面这两个侧面时，我们将这两个侧面展开所得到的平面图形如图2所示，则BE=CE+BC=20+5=25，AE=10。在Rt△ABE中，由勾股定理，可得AB²=BE²+AE²=25²+10²=725。

③当蚂蚁爬行经过长方体的上表面与后面这两个侧面时，我们将这两个侧面展开所得到的平面图形如图3所示，则BC=5，AC=CD+AD=20+10=30。在Rt△ABC中，由勾股定理，可得AB²=BC²+AC²=5²+30²=925。
∵625＜725＜925，AB＞0，
∴蚂蚁爬行的路线经过长方体的右侧表面与前面这两个侧面时，蚂蚁爬行的路程最短，最短路程为25。