第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
3. 如图是由边长为 $1$ 的小正方形组成的方格图。
(1) 请在方格图中建立平面直角坐标系,使点 $A$ 的坐标为 $(3,3)$,点 $B$ 的坐标为 $(-1,0)$。
(2) 在 $x$ 轴上画点 $C$,使 $\triangle ABC$ 成为以 $AB$ 为腰的等腰三角形,并写出所有满足条件的点 $C$ 的坐标。(要求标出点 $C$ 的位置)

(1) 请在方格图中建立平面直角坐标系,使点 $A$ 的坐标为 $(3,3)$,点 $B$ 的坐标为 $(-1,0)$。
(2) 在 $x$ 轴上画点 $C$,使 $\triangle ABC$ 成为以 $AB$ 为腰的等腰三角形,并写出所有满足条件的点 $C$ 的坐标。(要求标出点 $C$ 的位置)

答案:
解:(1)略。(2)以 AB 为腰的等腰三角形有△ABC₁,△ABC₂,△ABC₃,其中点 C 的坐标分别为 C₁(-6,0),C₂(4,0),C₃(7,0)。
4. 一个质点在第一象限及 $x$ 轴、$y$ 轴上运动,在第 $1s$,它从原点运动到 $(0,1)$,然后接着按图中箭头所示方向运动 [即 $(0,0)\to(0,1)\to(1,1)\to(1,0)…\to$ ],且每秒移动 $1$ 个单位长度,那么第 $99s$ 时质点所在位置的坐标是多少?请写出推理过程。
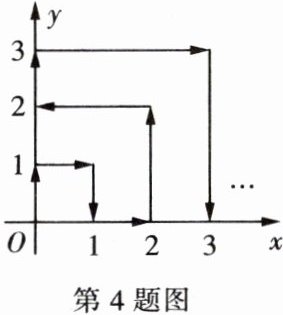

答案:
解:坐标为(9,0)。理由:用表格列出质点的运动规律:
运动时间/s
3=2²-1
8=3²-1
15=4²-1
24=5²-1
…
所在位置坐标
(1,0)
(0,2)
(3,0)
(0,4)
…
由表格可知,当运动时间为(n²-1)s 时,若 n 为偶数,则位于点(n-1,0);若 n 为奇数,则位于点(0,n-1)。
∵99=10²-1,
∴第 99 s 时质点所在位置的坐标是(9,0)。
运动时间/s
3=2²-1
8=3²-1
15=4²-1
24=5²-1
…
所在位置坐标
(1,0)
(0,2)
(3,0)
(0,4)
…
由表格可知,当运动时间为(n²-1)s 时,若 n 为偶数,则位于点(n-1,0);若 n 为奇数,则位于点(0,n-1)。
∵99=10²-1,
∴第 99 s 时质点所在位置的坐标是(9,0)。
5. 在平面直角坐标系中,对于 $P$,$Q$ 两点给出如下定义:若点 $P$ 到 $x$,$y$ 轴的距离中的最大值等于点 $Q$ 到 $x$,$y$ 轴的距离中的最大值,则称 $P$,$Q$ 两点为“等距点”。如图中的 $P$,$Q$ 两点即为“等距点”。
(1) 已知点 $A$ 的坐标为 $(-3,1)$。
①在点 $E(0,3)$,$F(3,-3)$,$G(2,-5)$ 中,判断点 $A$ 的“等距点”有哪些点;
②若点 $B$ 的坐标为 $B(m,m + 6)$,且 $A$,$B$ 两点为“等距点”,求点 $B$ 的坐标。
(2) 若 $T_1(-1,-k - 3)$,$T_2(4,4k - 3)$ 两点为“等距点”,求 $k$ 的值。
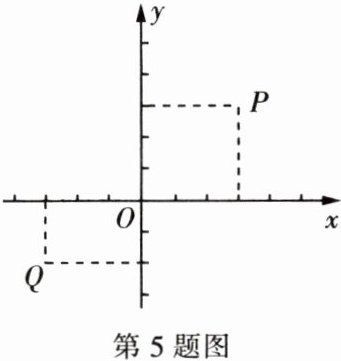
(1) 已知点 $A$ 的坐标为 $(-3,1)$。
①在点 $E(0,3)$,$F(3,-3)$,$G(2,-5)$ 中,判断点 $A$ 的“等距点”有哪些点;
②若点 $B$ 的坐标为 $B(m,m + 6)$,且 $A$,$B$ 两点为“等距点”,求点 $B$ 的坐标。
(2) 若 $T_1(-1,-k - 3)$,$T_2(4,4k - 3)$ 两点为“等距点”,求 $k$ 的值。

答案:
解:(1)①
∵点 A(-3,1)到 x,y 轴的距离中的最大值为 3,
∴与点 A 是“等距点”的点是 E,F。②点 B 到 x,y 轴的距离中至少有一个为 3 的点有(3,9),(-3,3),(-9,-3),这些点中与是点 A 的“等距点”的是(-3,3)。(2)
∵T₁(-1,-k-3),T₂(4,4k-3)两点为“等距点”,则分下列两种情况:①若|4k-3|≤4 时,则 4=-k-3 或-4=-k-3,解得 k=1 或 k=-7(舍去);②若|4k-3|>4 时,则|4k-3|=|-k-3|,解得 k=2 或 k=0(舍去)。综上所述,k 的值是 1 或 2。
∵点 A(-3,1)到 x,y 轴的距离中的最大值为 3,
∴与点 A 是“等距点”的点是 E,F。②点 B 到 x,y 轴的距离中至少有一个为 3 的点有(3,9),(-3,3),(-9,-3),这些点中与是点 A 的“等距点”的是(-3,3)。(2)
∵T₁(-1,-k-3),T₂(4,4k-3)两点为“等距点”,则分下列两种情况:①若|4k-3|≤4 时,则 4=-k-3 或-4=-k-3,解得 k=1 或 k=-7(舍去);②若|4k-3|>4 时,则|4k-3|=|-k-3|,解得 k=2 或 k=0(舍去)。综上所述,k 的值是 1 或 2。
6. (2023·衢州) 在如图所示的方格纸上建立适当的平面直角坐标系,若点 $A$ 的坐标为 $(0,1)$,点 $B$ 的坐标为 $(2,2)$,则点 $C$ 的坐标为______。
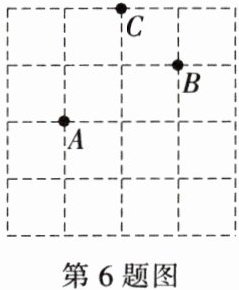

答案:
(1,3)
查看更多完整答案,请扫码查看


