第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 在美术字中,有些汉字是轴对称图形,下面四个汉字中,可以看作是轴对称图形的是 ( )


答案:
A
2. 画出下列文字、字母的对称轴.


答案:
答案略
3. 如图是一个英语单词的一部分,该单词关于直线l对称,请把它补齐,这个单词所指的物品是_____.


答案:
补全后的单词为“DOOR”,该单词所指的物品是门。
门
门
4. 我国最隆重最富有特色的传统节日之一的“春节”申遗成功,“春节”被纳入联合国教科文组织非物质文化遗产名录和项目. 过春节贴窗花是我国古老的习俗. 窗花将吉祥事物、美好愿望表现得淋漓尽致,将节日装点得红火富丽、喜气洋洋. 如图①②是民间一些老艺人剪出的窗花. 请你拿圆形纸片按下列要求剪窗花.
(1)对折一次,剪出一种窗花;
(2)对折一次,剪出一种窗花,窗花里包含轴对称的美术字;
(3)对折2次剪出一种窗花.
(1)对折一次,剪出一种窗花;
(2)对折一次,剪出一种窗花,窗花里包含轴对称的美术字;
(3)对折2次剪出一种窗花.

答案:
(1)
将圆形纸片沿一条直径对折,然后在纸上设计出简单的图案(如半圆、三角形等组合),沿着设计好的图案边缘剪下,展开后即可得到一种窗花。
(2)
将圆形纸片沿一条直径对折,在纸上设计出轴对称的美术字(如“囍”字的一半),再在周围设计一些对称的装饰图案(如花朵、叶子等),沿着设计好的图案边缘剪下,展开后就得到包含轴对称美术字的窗花。
(3)
将圆形纸片先沿一条直径对折,再沿与第一次折痕垂直的直径对折一次,然后在纸上设计图案(如多瓣花朵等),沿着设计好的图案边缘剪下,展开后就得到一种窗花。
(1)
将圆形纸片沿一条直径对折,然后在纸上设计出简单的图案(如半圆、三角形等组合),沿着设计好的图案边缘剪下,展开后即可得到一种窗花。
(2)
将圆形纸片沿一条直径对折,在纸上设计出轴对称的美术字(如“囍”字的一半),再在周围设计一些对称的装饰图案(如花朵、叶子等),沿着设计好的图案边缘剪下,展开后就得到包含轴对称美术字的窗花。
(3)
将圆形纸片先沿一条直径对折,再沿与第一次折痕垂直的直径对折一次,然后在纸上设计图案(如多瓣花朵等),沿着设计好的图案边缘剪下,展开后就得到一种窗花。
5. 现有如图①所示的两种瓷砖,用这两种瓷砖各2块,可设计出美丽的图案,如图②. 请同学们利用图②所示的基本图案,通过平移和轴对称,设计出一个更加美丽、更加大型的图案.
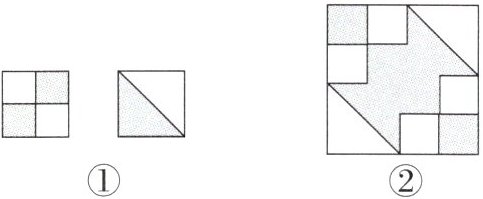

答案:
本题可根据平移和轴对称的性质,利用给定的基本图案设计出新的图案。
步骤一:明确平移和轴对称的性质
平移:是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动。平移不改变图形的形状和大小。
轴对称:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
步骤二:设计图案
将图②所示的基本图案进行如下操作:
平移操作:将基本图案分别向右平移$2$个基本图案的宽度,再向下平移$2$个基本图案的高度。
轴对称操作:以经过基本图案水平方向中点的竖直直线为对称轴,作出平移后图案的轴对称图形;再以经过基本图案竖直方向中点的水平直线为对称轴,作出上述所得图案的轴对称图形。
这样就得到了一个更加美丽、更加大型的图案。(由于本题要求不画图,此处仅描述设计思路)
综上,按照上述平移和轴对称的操作可设计出符合要求的图案。
步骤一:明确平移和轴对称的性质
平移:是指在平面内,将一个图形上的所有点都按照某个方向作相同距离的移动。平移不改变图形的形状和大小。
轴对称:如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
步骤二:设计图案
将图②所示的基本图案进行如下操作:
平移操作:将基本图案分别向右平移$2$个基本图案的宽度,再向下平移$2$个基本图案的高度。
轴对称操作:以经过基本图案水平方向中点的竖直直线为对称轴,作出平移后图案的轴对称图形;再以经过基本图案竖直方向中点的水平直线为对称轴,作出上述所得图案的轴对称图形。
这样就得到了一个更加美丽、更加大型的图案。(由于本题要求不画图,此处仅描述设计思路)
综上,按照上述平移和轴对称的操作可设计出符合要求的图案。
6. 问题情境:
数学活动课上,老师提出这样一个问题:等腰三角形底边的中点到两腰的距离相等吗?同学们就这个问题展开探究.
问题初探:
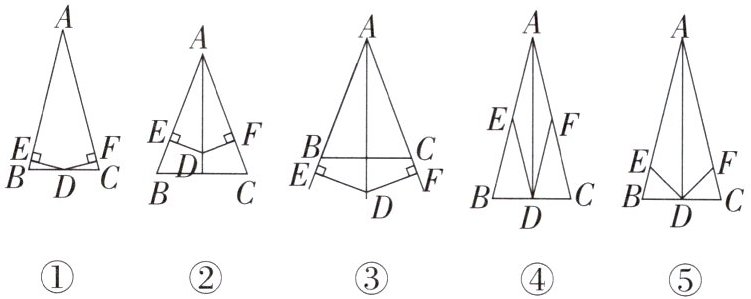
(1)希望小组的同学根据题意画出了相应的图形,如图①,在△ABC中,AB= AC,点D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E,F. 经过合作,该小组的同学得出的结论是DE= DF,他们的证法如下:
证明:∵DE⊥AB,DF⊥AC,
∴∠DEB= ∠DFC= 90°.
∵AB= AC,∴∠B= ∠C(依据1).
∵点D是BC的中点,∴BD= CD.
在△BDE和△CDF中,$\begin{cases} ∠DEB= ∠DFC, \\ ∠B= ∠C, \\ BD= CD, \end{cases} $
∴△BDE≌△CDF(依据2).
∴DE= DF.
a. 请写出依据1和依据2的内容:
依据1:______.
依据2:______.
b. 请你写出一种不同于希望小组的证法.
问题再探:
(2)若将底边上的中点D沿对称轴移动到其他位置(不与点A重合),如图②③,其他条件不变,DE与DF还相等吗?不需写出过程.
探究结论:
(3)根据以上探究可以得到______.
类比探究:
(4)奋斗小组的同学认真研究过后,发现了以下两个正确结论:a. 如图④,若DE,DF分别是△ABD和△ACD的中线,则DE= DF;b. 如图⑤,若DE,DF分别是△ABD和△ACD的角平分线,则DE= DF. 请你选择其中一个结论,写出证明过程.
数学活动课上,老师提出这样一个问题:等腰三角形底边的中点到两腰的距离相等吗?同学们就这个问题展开探究.
问题初探:
(1)希望小组的同学根据题意画出了相应的图形,如图①,在△ABC中,AB= AC,点D是BC的中点,DE⊥AB,DF⊥AC,垂足分别为点E,F. 经过合作,该小组的同学得出的结论是DE= DF,他们的证法如下:
证明:∵DE⊥AB,DF⊥AC,
∴∠DEB= ∠DFC= 90°.
∵AB= AC,∴∠B= ∠C(依据1).
∵点D是BC的中点,∴BD= CD.
在△BDE和△CDF中,$\begin{cases} ∠DEB= ∠DFC, \\ ∠B= ∠C, \\ BD= CD, \end{cases} $
∴△BDE≌△CDF(依据2).
∴DE= DF.
a. 请写出依据1和依据2的内容:
依据1:______.
依据2:______.
b. 请你写出一种不同于希望小组的证法.
问题再探:
(2)若将底边上的中点D沿对称轴移动到其他位置(不与点A重合),如图②③,其他条件不变,DE与DF还相等吗?不需写出过程.
探究结论:
(3)根据以上探究可以得到______.
类比探究:
(4)奋斗小组的同学认真研究过后,发现了以下两个正确结论:a. 如图④,若DE,DF分别是△ABD和△ACD的中线,则DE= DF;b. 如图⑤,若DE,DF分别是△ABD和△ACD的角平分线,则DE= DF. 请你选择其中一个结论,写出证明过程.

答案:
(1)a. 依据1:等边对等角;依据2:AAS
b. 证明:连接AD,
∵AB=AC,点D是BC的中点,
∴AD平分∠BAC(等腰三角形三线合一),
∵DE⊥AB,DF⊥AC,
∴DE=DF(角平分线上的点到角两边的距离相等)
(2)相等
(3)等腰三角形对称轴上任意一点(不与顶点重合)到两腰的距离相等
(4)选择a证明:
∵AB=AC,D在等腰△ABC的对称轴上,
∴∠BAD=∠CAD,AD=AD,
∴△ABD≌△ACD(SAS),
∴BD=CD,AB=AC。
∵DE,DF分别是△ABD,△ACD的中线,
∴E,F分别为AB,AC中点,
∴BE=AB/2,CF=AC/2,
∵AB=AC,
∴BE=CF。在△BDE和△CDF中,BE=CF,∠B=∠C(AB=AC),BD=CD,
∴△BDE≌△CDF(SAS),
∴DE=DF
(1)a. 依据1:等边对等角;依据2:AAS
b. 证明:连接AD,
∵AB=AC,点D是BC的中点,
∴AD平分∠BAC(等腰三角形三线合一),
∵DE⊥AB,DF⊥AC,
∴DE=DF(角平分线上的点到角两边的距离相等)
(2)相等
(3)等腰三角形对称轴上任意一点(不与顶点重合)到两腰的距离相等
(4)选择a证明:
∵AB=AC,D在等腰△ABC的对称轴上,
∴∠BAD=∠CAD,AD=AD,
∴△ABD≌△ACD(SAS),
∴BD=CD,AB=AC。
∵DE,DF分别是△ABD,△ACD的中线,
∴E,F分别为AB,AC中点,
∴BE=AB/2,CF=AC/2,
∵AB=AC,
∴BE=CF。在△BDE和△CDF中,BE=CF,∠B=∠C(AB=AC),BD=CD,
∴△BDE≌△CDF(SAS),
∴DE=DF
查看更多完整答案,请扫码查看


