《2025年名校作业八年级数学上册人教版湖北专版》

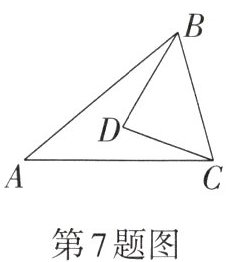
7.【教材P17习题T9变式】如图,在△ABC中,点D在△ABC内,∠A= 40°,∠ABD= ∠ACD= 20°,则∠BDC的度数为______.


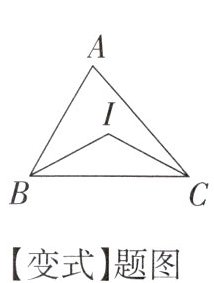
【变式】如图,在△ABC中,BI,CI分别平分∠ABC,∠ACB.若∠I= 125°,则∠A的度数为______.

答案： $80^\circ$；$70^\circ$。

8.如图,在△ABC中,∠A= 50°,点E,F分别在边AB,AC上,将△ABC沿EF折叠得到△DEF,则∠1+∠2的度数是______.

答案： 在△ABC中，∠A=50°，E、F分别在AB、AC上，沿EF折叠△ABC得△DEF，由折叠性质知∠AEF=∠DEF，∠AFE=∠DFE，∠D=∠A=50°。
设∠AEF=∠DEF=x，∠AFE=∠DFE=y。
在△AEF中，∠A+∠AEF+∠AFE=180°，即50°+x+y=180°，得x+y=130°。
在直线AB上，∠AEB=180°，则∠AEF+∠DEF+∠1=180°，即x+x+∠1=180°，得∠1=180°-2x。
在直线AC上，∠AFC=180°，则∠AFE+∠DFE+∠2=180°，即y+y+∠2=180°，得∠2=180°-2y。
∠1+∠2=(180°-2x)+(180°-2y)=360°-2(x+y)=360°-2×130°=100°。
100°

9.若在一个三角形中,一个内角是另一个内角的3倍,则我们称这样的三角形为"3倍角三角形".例如,三个内角分别为120°,40°,20°的三角形是"3倍角三角形".
(1)若在△ABC中,∠A= 35°,∠B= 40°,则△ABC______"3倍角三角形".(填"是"或"不是")
(2)若△ABC是"3倍角三角形",且∠B= 30°,求△ABC中最小内角的度数.

答案：
(1) 是；
(2) 10°或30°

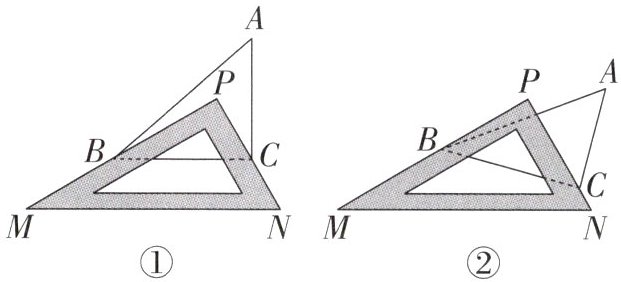
10.如图①,将含30°角的直角三角尺PMN放置在△ABC上(点P在△ABC内),三角尺PMN的两条直角边PM,PN恰好分别经过点B,C.探究∠ABP与∠ACP之间的数量关系.
(1)特殊探究:如图①,∠PBC+∠PCB= ______,若∠A= 50°,则∠ABP+∠ACP= ______.
(2)类比探究:请类比(1),探究如图①中∠ABP+∠ACP与∠A的关系.
(3)延伸探究:如图②,改变直角三角尺PMN的位置,使点P在△ABC外,三角尺PMN的两条直角边PM,PN仍然分别经过点B,C,则(2)中的结论是否仍然成立? 若成立,请给予证明;若不成立,请写出结论,并说明理由.

答案：
(1) 90°；40°
(2) ∠ABP + ∠ACP = 90° - ∠A
(3) 不成立，结论：∠ABP + ∠ACP = ∠A - 90°。
理由：在△ABC中，∠ABC + ∠ACB = 180° - ∠A。在△PBC中，∠PBC + ∠PCB = 180° - ∠BPC = 90°。点P在△ABC外时，∠PBC = ∠ABC + ∠ABP，∠PCB = ∠ACB + ∠ACP，故∠ABC + ∠ABP + ∠ACB + ∠ACP = 90°，即(180° - ∠A) + (∠ABP + ∠ACP) = 90°，因此∠ABP + ∠ACP = ∠A - 90°。