《2025年名校作业八年级数学上册人教版湖北专版》

6.下列数据能唯一确定三角形的形状和大小的是 ( )

A.AB= 4,BC= 5,∠C= 60°
B.AB= 6,∠C= 60°,∠B= 70°
C.AB= 4,BC= 5,AC= 10
D.∠C= 60°,∠B= 70°,∠A= 50°

答案： B

7.如图,点C,E分别为△ABD的边BD,AB上的点,AE= AD,CE= CD.若∠D= 80°,∠ECD= 130°,则∠B的度数为______.

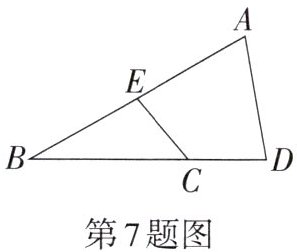
答案： 连接AC。
在△AEC和△ADC中，
∵AE=AD，CE=CD，AC=AC，
∴△AEC≌△ADC（SSS）。
∴∠AEC=∠D=80°，∠ACE=∠ACD。
∵点C在BD上，∠ECD=130°，
∴∠BCE=180°-∠ECD=180°-130°=50°。
∵∠AEC是△BEC的外角，
∴∠AEC=∠B+∠BCE。
∴80°=∠B+50°，
∴∠B=30°。
30°

8.如图,已知AB= AC,AD= AE,BD= CE,且∠1= 30°,∠2= 35°,则∠3的度数为______.

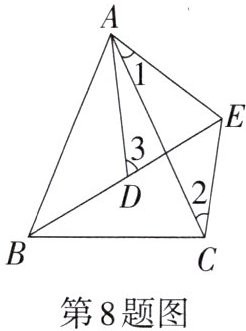
答案： 在△ABD和△ACE中，
∵AB=AC，AD=AE，BD=CE，
∴△ABD≌△ACE（SSS），
∴∠ADB=∠AEC，∠ABD=∠ACE。
∵∠1=30°，∠2=35°，
∴∠BAD=∠1=30°，∠ACE=∠2=35°，
∴∠ABD=∠ACE=35°。
在△ABD中，∠ADB=180°-∠BAD-∠ABD=180°-30°-35°=115°，
∴∠AEC=∠ADB=115°。
∵∠AEC是△CDE的外角，
∴∠AEC=∠3+∠ECD，
∵∠ECD=∠2=35°，
∴∠3=∠AEC-∠ECD=115°-35°=80°。
80°

9.如图,AB= DC,BM= CM,AC= DB.求证:AM= DM.

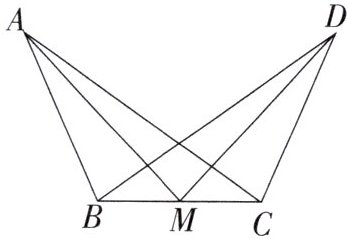
答案： 证明：
连接$AD$。
在$\triangle ABD$和$\triangle DCA$中：
$AB = DC$，
$BD = AC$，
$AD = DA$（公共边）。
所以，$\triangle ABD\cong \triangle DCA(SSS)$。
所以$\angle BDA = \angle CAD$。
在$\triangle ADM$和$\triangle DAM$中：
$AD = DA$（公共边），
$\angle BDA = \angle CAD$，
$BM = CM$。
所以，$\triangle ADM\cong \triangle DAM(SAS)$。
所以，$AM = DM$。

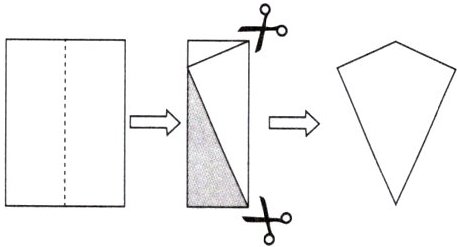
10.综合与实践
定义:两组邻边分别相等的四边形叫作“筝形”.
我们研究一种新几何图形的一般过程是先学习定义,再研究性质和判定.而性质的研究,其实就是对图形边、角、对角线等基本要素的研究.八年级某班按照这样的思路对“筝形”的性质展开了研究:
第一步:根据定义剪出一个“筝形”;
第二步:用测量、折纸等方法猜想“筝形”边、角、对角线的结论;
第三步:通过证明得到性质.
解答问题:
(1)猜想“筝形”的对角线有什么性质,请画出图形,写出已知,并证明.(写出一条即可)
(2)从性质进一步探究可得到“筝形”的面积公式,请直接写出“筝形”的面积公式.

答案：
(1)猜想：筝形的一条对角线垂直平分另一条对角线。
图形：画出筝形ABCD，其中AB=AD，BC=CD，连接对角线AC、BD交于点O。
已知：在筝形ABCD中，AB=AD，BC=CD，对角线AC、BD交于点O。
求证：AC垂直平分BD。
证明：在△ABC和△ADC中，
∵AB=AD（已知），BC=CD（已知），AC=AC（公共边），
∴△ABC≌△ADC（SSS）。
∴∠BAC=∠DAC（全等三角形对应角相等）。
在△ABO和△ADO中，
∵AB=AD（已知），∠BAO=∠DAO（已证），AO=AO（公共边），
∴△ABO≌△ADO（SAS）。
∴BO=DO，∠AOB=∠AOD（全等三角形对应边、对应角相等）。
∵∠AOB+∠AOD=180°（平角定义），
∴∠AOB=∠AOD=90°，即AC⊥BD。
∴AC垂直平分BD。
(2)筝形的面积公式：对角线乘积的一半，即$S=\frac{1}{2}d_1d_2$（其中$d_1$、$d_2$为两条对角线的长度）。