《2025年名校作业八年级数学上册人教版湖北专版》

8. 若等腰三角形的一个外角是100°,则其底角是______.

答案： D（假设选项D为$80^{\circ}$或$50^{\circ}$ ，这里主要关注解题过程和结果，选项字母按常规设置）

9. 若等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角为______.

答案： 60°或120°

10. 在△OPQ中,OP= OQ,OP的垂直平分线交OP于点D,交直线OQ于点E. 若∠OEP= 50°,则∠POQ的度数为______.

答案： 65°或115°

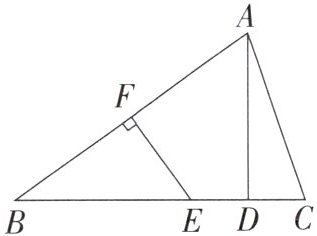
11. 如图,在△ABC中,AB的垂直平分线EF交BC于点E,交AB于点F,点D为CE的中点,BE= AC.
(1)求证：AD⊥BC.
(2)若∠BAC= 75°,求∠B的度数.

答案：
(1)证明：
∵EF是AB的垂直平分线，
∴EA=EB（线段垂直平分线上的点到两端点距离相等）。
∵BE=AC，
∴EA=AC（等量代换），
∴△EAC是等腰三角形。
∵D是CE的中点，
∴AD是△EAC底边CE上的中线（中点定义）。
由等腰三角形三线合一性质，底边上的中线也是底边上的高，
∴AD⊥CE，即AD⊥BC。
(2)设∠B=x。
∵EA=EB，
∴∠EAB=∠B=x（等边对等角），
∴∠AEB=180°-2x（三角形内角和定理）。
∵∠AEB+∠AEC=180°（邻补角定义），
∴∠AEC=180°-(180°-2x)=2x。
∵EA=AC，
∴∠AEC=∠ACE=2x（等边对等角）。
在△ABC中，∠BAC+∠B+∠ACB=180°（三角形内角和定理），
即75°+x+2x=180°，解得3x=105°，x=35°。
∴∠B=35°。

12. 如图,在△ABC中,AC= BC,点D是AB边上一点,过点D作DE⊥BC于点E,过点E作EF⊥AC于点F.
(1)若∠ADE= 160°,求∠DEF的度数.
(2)若点D是AB边的中点,求证：∠BDE= $\frac{1}{2}$∠ACB.

答案：
(1)
∵AC=BC，
∴∠A=∠B．
∵DE⊥BC，
∴∠DEB=90°．
∵∠ADE=160°，∠ADE+∠EDB=180°，
∴∠EDB=20°．
在△BDE中，∠B=180°-∠DEB-∠EDB=180°-90°-20°=70°．
∴∠A=∠B=70°，在△ABC中，∠ACB=180°-∠A-∠B=40°．
∵EF⊥AC，
∴∠EFC=90°，在△EFC中，∠FEC=180°-∠EFC-∠ACB=180°-90°-40°=50°．
∵DE⊥BC，∠DEC=90°，∠DEC=∠DEF+∠FEC，
∴∠DEF=90°-50°=40°．
(2)证明：
∵AC=BC，D是AB中点，
∴CD平分∠ACB，CD⊥AB（等腰三角形三线合一）．
∴∠BCD=1/2∠ACB，∠CDB=90°．
∵DE⊥BC，
∴∠DEB=90°．
在△BDE中，∠BDE=90°-∠B．
在△BCD中，∠BCD=90°-∠B．
∴∠BDE=∠BCD=1/2∠ACB，即∠BDE=1/2∠ACB．

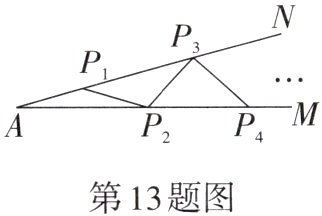
13. 如图,在一钢架NAM中,∠A= 15°,现要在角的内部焊上等长的钢条(相邻钢条首尾相接)加固钢架. 若$AP_1= P_1P_2= P_2P_3=… ,$则这样的钢条最多能焊( )

A.4根
B.5根
C.6根
D.7根

答案： 解题步骤：
1. 设钢条长度：设 $ AP_1 = P_1P_2 = P_2P_3 = P_3P_4 = \cdots = x $。
2. 第一个等腰三角形：在 $ \triangle AP_1P_2 $ 中，$ AP_1 = P_1P_2 = x $，$ \angle A = 15^\circ $，由等边对等角得 $ \angle AP_2P_1 = 15^\circ $。
外角 $ \angle P_1P_2M = \angle A + \angle AP_2P_1 = 15^\circ + 15^\circ = 30^\circ $。
3. 第二个等腰三角形：在 $ \triangle P_1P_2P_3 $ 中，$ P_1P_2 = P_2P_3 = x $，$ \angle P_2P_1P_3 = \angle P_2P_3P_1 = 30^\circ $。
外角 $ \angle P_2P_3N = \angle P_1P_2P_3 + \angle P_1P_3P_2 = 30^\circ + 30^\circ = 60^\circ $。
4. 第三个等腰三角形：在 $ \triangle P_2P_3P_4 $ 中，$ P_2P_3 = P_3P_4 = x $，$ \angle P_3P_2P_4 = \angle P_3P_4P_2 = 60^\circ $。
外角 $ \angle P_3P_4M = \angle P_2P_3P_4 + \angle P_2P_4P_3 = 60^\circ + 60^\circ = 120^\circ $。
5. 第四个等腰三角形：在 $ \triangle P_3P_4P_5 $ 中，$ P_3P_4 = P_4P_5 = x $，$ \angle P_4P_3P_5 = \angle P_4P_5P_3 = 120^\circ $。
此时内角和 $ 120^\circ + 120^\circ = 240^\circ ＞ 180^\circ $，无法构成三角形。
6. 钢条数量：可构成的钢条为 $ P_1P_2, P_2P_3, P_3P_4, P_4P_5 $，共4根。
最终结论
A.4根

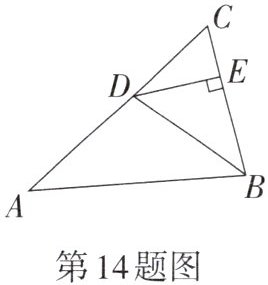
14. 如图,在△ABC中,∠A= 40°,∠C= 60°,D为AC边上一点,过点D作DE⊥BC于点E. 若AD= BD,BE= 2,则AB的长为______.

答案： 1. 在△ABC中，∠A=40°，∠C=60°，
∴∠ABC=180°-∠A-∠C=80°。
2.
∵AD=BD，
∴△ABD为等腰三角形，
∴∠ABD=∠A=40°。
3.
∴∠DBC=∠ABC-∠ABD=80°-40°=40°，即BD平分∠ABC。
4. 过点D作DF⊥AB于F，
∵BD平分∠ABC，DE⊥BC，
∴DF=DE（角平分线上的点到角两边距离相等）。
5. 在Rt△BDF和Rt△BDE中，$\left\{\begin{array}{l} BD=BD\\ DF=DE\end{array}\right.$，
∴Rt△BDF≌Rt△BDE（HL），
∴BF=BE=2。
6.
∵AD=BD，DF⊥AB，
∴F为AB中点（等腰三角形三线合一），
∴AB=2BF=4。
4