第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
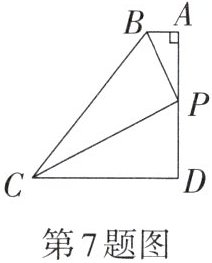
7. 【教材P53习题T8变式】如图,AB//CD,BP和CP分别平分∠ABC和∠BCD,AD经过点P,且AD⊥AB. 若AD= 10,则点P到BC的距离是______.

答案:
过点P作PE⊥BC于E。
∵AB//CD,AD⊥AB,
∴AD⊥CD(垂直于平行线中的一条,必垂直于另一条),∠A=∠D=90°。
∵BP平分∠ABC,PA⊥AB,PE⊥BC,
∴PA=PE(角平分线上的点到角两边距离相等)。
∵CP平分∠BCD,PD⊥CD,PE⊥BC,
∴PD=PE(角平分线上的点到角两边距离相等)。
设PE=h,则PA=PD=h。
∵AD=PA+PD,AD=10,
∴h+h=10,解得h=5。
点P到BC的距离是5。
5
∵AB//CD,AD⊥AB,
∴AD⊥CD(垂直于平行线中的一条,必垂直于另一条),∠A=∠D=90°。
∵BP平分∠ABC,PA⊥AB,PE⊥BC,
∴PA=PE(角平分线上的点到角两边距离相等)。
∵CP平分∠BCD,PD⊥CD,PE⊥BC,
∴PD=PE(角平分线上的点到角两边距离相等)。
设PE=h,则PA=PD=h。
∵AD=PA+PD,AD=10,
∴h+h=10,解得h=5。
点P到BC的距离是5。
5
8. 如图,在△ABC中,∠ACB= 90°,BC= 6,AC= 8,CE是△ABC的角平分线,过点E作EF//AC交BC于点F,则EF的长为______.


答案:
在△ABC中,∠ACB=90°,AC=8,BC=6,由勾股定理得AB=√(AC²+BC²)=√(8²+6²)=10。
CE是∠ACB的平分线,∠ACB=90°,则∠ACE=∠BCE=45°。
∵EF//AC,
∴∠CEF=∠ACE=45°(内错角相等)。
在△CEF中,∠ECF=∠CEF=45°,
∴CF=EF(等角对等边)。
设EF=x,则CF=x,BF=BC-CF=6-x。
∵EF//AC,
∴△BEF∽△BAC(AA相似)。
∴EF/AC=BF/BC,即x/8=(6-x)/6。
解得6x=8(6-x),6x=48-8x,14x=48,x=24/7。
EF=24/7。
CE是∠ACB的平分线,∠ACB=90°,则∠ACE=∠BCE=45°。
∵EF//AC,
∴∠CEF=∠ACE=45°(内错角相等)。
在△CEF中,∠ECF=∠CEF=45°,
∴CF=EF(等角对等边)。
设EF=x,则CF=x,BF=BC-CF=6-x。
∵EF//AC,
∴△BEF∽△BAC(AA相似)。
∴EF/AC=BF/BC,即x/8=(6-x)/6。
解得6x=8(6-x),6x=48-8x,14x=48,x=24/7。
EF=24/7。
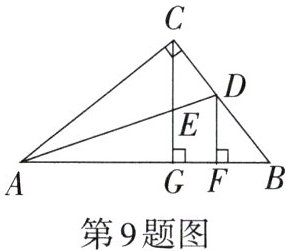
9. 如图,在Rt△ABC中,∠ACB= 90°,AD平分∠BAC交BC于点D,CG⊥AB于点G,交AD于点E,DF⊥AB于点F. 给出下列结论:①DC= DF;②∠CED= ∠CDE;③∠ADF= 2∠FDB;④S△AEC:S△AEG= AC:AG. 其中正确的是______.(填序号)

答案:
①
∵AD平分∠BAC,∠ACB=90°,DF⊥AB,
∴DC=DF(角平分线性质),①正确;
②
∵CG⊥AB,
∴∠AGE=90°,设∠CAD=∠BAD=α,则∠AEG=90°-α(Rt△AEG中),∠CED=∠AEG=90°-α(对顶角);∠ACB=90°,
∴∠ADC=90°-α(Rt△ACD中),即∠CDE=90°-α,
∴∠CED=∠CDE,②正确;
③∠ADF=90°-α(Rt△ADF中),∠B=90°-2α,∠FDB=∠B=90°-2α(Rt△DFB中,DF=DC,∠DFB=90°),90°-α=2(90°-2α)不恒成立,③错误;
④S△AEC:S△AEG=(1/2·AC·AE·sinα):(1/2·AG·AE·sinα)=AC:AG,④正确。
①②④
∵AD平分∠BAC,∠ACB=90°,DF⊥AB,
∴DC=DF(角平分线性质),①正确;
②
∵CG⊥AB,
∴∠AGE=90°,设∠CAD=∠BAD=α,则∠AEG=90°-α(Rt△AEG中),∠CED=∠AEG=90°-α(对顶角);∠ACB=90°,
∴∠ADC=90°-α(Rt△ACD中),即∠CDE=90°-α,
∴∠CED=∠CDE,②正确;
③∠ADF=90°-α(Rt△ADF中),∠B=90°-2α,∠FDB=∠B=90°-2α(Rt△DFB中,DF=DC,∠DFB=90°),90°-α=2(90°-2α)不恒成立,③错误;
④S△AEC:S△AEG=(1/2·AC·AE·sinα):(1/2·AG·AE·sinα)=AC:AG,④正确。
①②④
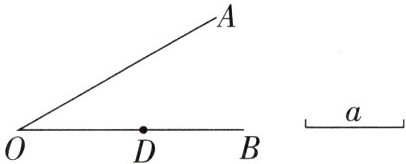
10. 如图,已知∠AOB和线段a,点D为OB上的一点.
(1)作∠AOB的平分线OC.
(2)在OC上取一点P,使OP= a,连接PD.
(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OA上取一点E,使PE= PD. 这时他发现∠OEP与∠ODP之间存在一定的数量关系,请写出∠OEP与∠ODP之间的数量关系,并说明理由.
(1)作∠AOB的平分线OC.
(2)在OC上取一点P,使OP= a,连接PD.
(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边OA上取一点E,使PE= PD. 这时他发现∠OEP与∠ODP之间存在一定的数量关系,请写出∠OEP与∠ODP之间的数量关系,并说明理由.

答案:
(1) 作图步骤:①以点O为圆心,任意长为半径画弧,分别交OA、OB于点M、N;②分别以点M、N为圆心,大于1/2MN的长为半径画弧,两弧在∠AOB内部交于点C;③作射线OC,OC即为∠AOB的平分线。
(2) 作图步骤:①用圆规量取线段a的长度;②以点O为圆心,a为半径画弧,交OC于点P;③连接PD。
(3) ∠OEP与∠ODP的数量关系为∠OEP=∠ODP或∠OEP+∠ODP=180°。
理由:过点P作PG⊥OA于G,PH⊥OB于H。
∵OC平分∠AOB,
∴PG=PH(角平分线性质)。
在Rt△PGE和Rt△PHD中,
∵PE=PD,PG=PH,
∴Rt△PGE≌Rt△PHD(HL),
∴∠PEG=∠PDH。
当点E在PG右侧(靠近A方向)时,∠OEP=∠PEG=∠PDH=∠ODP;
当点E在PG左侧(靠近O方向)时,∠OEP+∠PEG=180°,
∴∠OEP+∠ODP=180°。
(1) 作图步骤:①以点O为圆心,任意长为半径画弧,分别交OA、OB于点M、N;②分别以点M、N为圆心,大于1/2MN的长为半径画弧,两弧在∠AOB内部交于点C;③作射线OC,OC即为∠AOB的平分线。
(2) 作图步骤:①用圆规量取线段a的长度;②以点O为圆心,a为半径画弧,交OC于点P;③连接PD。
(3) ∠OEP与∠ODP的数量关系为∠OEP=∠ODP或∠OEP+∠ODP=180°。
理由:过点P作PG⊥OA于G,PH⊥OB于H。
∵OC平分∠AOB,
∴PG=PH(角平分线性质)。
在Rt△PGE和Rt△PHD中,
∵PE=PD,PG=PH,
∴Rt△PGE≌Rt△PHD(HL),
∴∠PEG=∠PDH。
当点E在PG右侧(靠近A方向)时,∠OEP=∠PEG=∠PDH=∠ODP;
当点E在PG左侧(靠近O方向)时,∠OEP+∠PEG=180°,
∴∠OEP+∠ODP=180°。
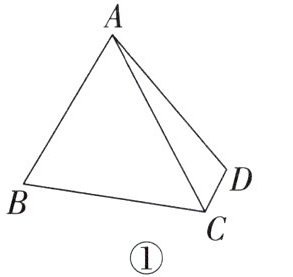
11. 已知在四边形ABCD中,∠ABC+∠ADC= 180°,AC平分∠BCD.
(1)如图①,求证:AB= AD.
(2)如图②,点F为BC上一点,延长AF到点E,连接CE,且CE= AD,∠BCE= ∠BAC-45°. 若∠BAD= 90°,求证:BF= EF.
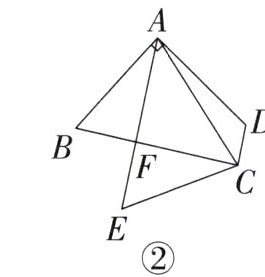
(1)如图①,求证:AB= AD.
(2)如图②,点F为BC上一点,延长AF到点E,连接CE,且CE= AD,∠BCE= ∠BAC-45°. 若∠BAD= 90°,求证:BF= EF.


答案:
(1)证明:
在$BC$上截取$CG=CD$,连接$AG$。
因为$AC$平分$\angle BCD$,
所以$\angle ACD=\angle ACG$。
在$\triangle ACD$和$\triangle ACG$中,
$\begin{cases}CD=CG,\\\angle ACD=\angle ACG,\\AC=AC.\end{cases}$
所以$\triangle ACD\cong\triangle ACG(SAS)$,
所以$AD=AG,\angle ADC=\angle AGC$。
因为$\angle ABC+\angle ADC=180^\circ,\angle AGB+\angle AGC=180^\circ$,
所以$\angle ABC=\angle AGB$,
所以$AB=AG$,
因此$AB=AD$。
(2)证明:
在$AE$上截取$AH=AC$,连接$CH$。
因为$\angle BAD=90^\circ,\angle ABC+\angle ADC=180^\circ$,
所以$\angle BCD=90^\circ$。
因为$AC$平分$\angle BCD$,
所以$\angle ACB=\angle ACD=45^\circ$。
因为$\angle BCE=\angle BAC-45^\circ$,
所以$\angle BAC=\angle BCE+\angle ACB=\angle ACE$。
因为$AB=AD=AG,AH=AC$,
所以$BH=CG$。
在$\triangle BAH$和$\triangle CAG$中,
$\begin{cases}BA=CA,\\BH=CG,\\AH=AG.\end{cases}$
所以$\triangle BAH\cong\triangle CAG(SSS)$,
所以$\angle BAH=\angle CAG$。
因为$\angle BAH+\angle HAC=\angle BAC,\angle HAC+\angle CAG=\angle HAG$,
所以$\angle HAG=\angle BAC$。
因为$\angle BAC=\angle ACE,\angle HAG=\angle E+\angle ACE$,
所以$\angle E=\angle ACE$,
所以$AE=CE$,
因此$AE=AD=CE$。
因为$CE=AD=AG,AH=AC$,
所以$EH=CG$。
因为$CG=BF$,
所以$EH=BF$。
在$\triangle EFH$和$\triangle CFB$中,
$\begin{cases}\angle E=\angle BCE,\\\angle EFH=\angle CFB,\\EH=BF.\end{cases}$
所以$\triangle EFH\cong\triangle CFB(AAS)$,
因此$EF=BF$。
在$BC$上截取$CG=CD$,连接$AG$。
因为$AC$平分$\angle BCD$,
所以$\angle ACD=\angle ACG$。
在$\triangle ACD$和$\triangle ACG$中,
$\begin{cases}CD=CG,\\\angle ACD=\angle ACG,\\AC=AC.\end{cases}$
所以$\triangle ACD\cong\triangle ACG(SAS)$,
所以$AD=AG,\angle ADC=\angle AGC$。
因为$\angle ABC+\angle ADC=180^\circ,\angle AGB+\angle AGC=180^\circ$,
所以$\angle ABC=\angle AGB$,
所以$AB=AG$,
因此$AB=AD$。
(2)证明:
在$AE$上截取$AH=AC$,连接$CH$。
因为$\angle BAD=90^\circ,\angle ABC+\angle ADC=180^\circ$,
所以$\angle BCD=90^\circ$。
因为$AC$平分$\angle BCD$,
所以$\angle ACB=\angle ACD=45^\circ$。
因为$\angle BCE=\angle BAC-45^\circ$,
所以$\angle BAC=\angle BCE+\angle ACB=\angle ACE$。
因为$AB=AD=AG,AH=AC$,
所以$BH=CG$。
在$\triangle BAH$和$\triangle CAG$中,
$\begin{cases}BA=CA,\\BH=CG,\\AH=AG.\end{cases}$
所以$\triangle BAH\cong\triangle CAG(SSS)$,
所以$\angle BAH=\angle CAG$。
因为$\angle BAH+\angle HAC=\angle BAC,\angle HAC+\angle CAG=\angle HAG$,
所以$\angle HAG=\angle BAC$。
因为$\angle BAC=\angle ACE,\angle HAG=\angle E+\angle ACE$,
所以$\angle E=\angle ACE$,
所以$AE=CE$,
因此$AE=AD=CE$。
因为$CE=AD=AG,AH=AC$,
所以$EH=CG$。
因为$CG=BF$,
所以$EH=BF$。
在$\triangle EFH$和$\triangle CFB$中,
$\begin{cases}\angle E=\angle BCE,\\\angle EFH=\angle CFB,\\EH=BF.\end{cases}$
所以$\triangle EFH\cong\triangle CFB(AAS)$,
因此$EF=BF$。
查看更多完整答案,请扫码查看


