《2025年名校作业八年级数学上册人教版湖北专版》

9.李老师有$[(n+5)^{2}-(n-1)^{2}](n≥1$,且n为整数)个礼物.现在将这些礼物平均分给班级的同学,恰好能分完.给出下列选项:①4人;②12人;③$(n+2)$人;④$(6n+8)$人.其中可以是班级同学人数的是______.(填序号)

答案： $\begin{aligned}&(n + 5)^2 - (n - 1)^2\\=&[(n + 5) + (n - 1)][(n + 5) - (n - 1)]\\=&(2n + 4)×6\\=&12(n + 2)\end{aligned}$
礼物总数为$12(n + 2)$（$n\geq1$，$n$为整数）。
①$12(n + 2)÷4 = 3(n + 2)$，为整数，符合；
②$12(n + 2)÷12 = n + 2$，为整数，符合；
③$12(n + 2)÷(n + 2) = 12$，为整数，符合；
④$12(n + 2)÷(6n + 8)=\frac{12n + 24}{6n + 8}=2 + \frac{8}{6n + 8}$，$6n + 8\geq14$（$n\geq1$），$\frac{8}{6n + 8}$不是整数，不符合。
①②③

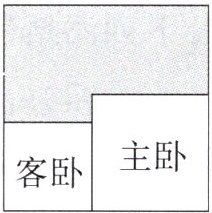
10.如图是某正方形房屋的结构平面图,其中主卧与客卧都为正方形.若其边长差为1米,其余部分(阴影部分)的面积为40平方米,则主卧与客卧的面积和为______平方米.
]

答案： 设主卧边长为$a$米，客卧边长为$b$米$(a ＞ b)$，由题意得$a - b = 1$。
设房屋（大正方形）边长为$x$米，阴影部分面积为40平方米。房屋面积等于主卧面积、客卧面积与阴影面积之和，即$x^2 = a^2 + b^2 + 40$。
由图形布局知，房屋边长$x = a + b$，则$x^2 = (a + b)^2$。
因此$(a + b)^2 = a^2 + b^2 + 40$，展开得$a^2 + 2ab + b^2 = a^2 + b^2 + 40$，化简得$2ab = 40$，即$ab = 20$。
因为$a - b = 1$，所以$(a - b)^2 = 1$，即$a^2 - 2ab + b^2 = 1$。
则$a^2 + b^2 = 1 + 2ab = 1 + 40 = 41$。
41

11.计算:
(1)$4(y+1)^{2}-(2y+3)(2y-3);$ (2)$(2x+y)^{2}-y(y+4x)+(-2x)^{2}.$

答案：
(1)
解：
首先利用完全平方公式展开$(y+1)^{2}$，得到：
$(y+1)^{2} = y^{2} + 2y + 1$
所以，
$4(y+1)^{2} = 4(y^{2} + 2y + 1) = 4y^{2} + 8y + 4$
接着利用平方差公式展开$(2y+3)(2y-3)$，得到：
$(2y+3)(2y-3) = 4y^{2} - 9$
将上述两部分结果代入原式，得：
$4(y+1)^{2}-(2y+3)(2y-3) = 4y^{2} + 8y + 4 - 4y^{2} + 9 = 8y + 13$
(2)
解：
首先利用完全平方公式展开$(2x+y)^{2}$，得到：
$(2x+y)^{2} = 4x^{2} + 4xy + y^{2}$
接着展开$y(y+4x)$，得到：
$y(y+4x) = y^{2} + 4xy$
将上述两部分以及$(-2x)^{2}$的结果代入原式，得：
$(2x+y)^{2}-y(y+4x)+(-2x)^{2} = 4x^{2} + 4xy + y^{2} - y^{2} - 4xy + 4x^{2} = 8x^{2}$

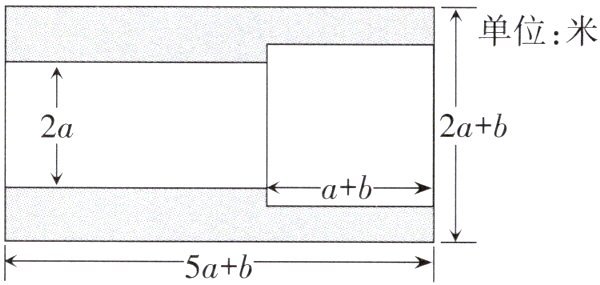
12.相关部门计划在某广场规划出一块长为$(5a+b)$米,宽为$(2a+b)$米的长方形地块,在其内部选取一块边长为$(a+b)$米的正方形地块用作活动宣传展区,并在左边修建一条宽为2a米的长方形步行街,其余部分为绿化场地,尺寸如图所示.
(1)用含a,b的代数式表示绿化的面积.(结果要化简)
(2)若$a= 2,b= 5$,请求出绿化的面积.
]

答案：
(1) 绿化面积=总面积-步行街面积-正方形展区面积
总面积=(5a+b)(2a+b)=10a²+7ab+b²
步行街面积=2a(2a+b)=4a²+2ab
正方形展区面积=(a+b)²=a²+2ab+b²
绿化面积=10a²+7ab+b²-(4a²+2ab)-(a²+2ab+b²)=5a²+3ab
(2) 当a=2,b=5时，
5a²+3ab=5×2²+3×2×5=20+30=50
(1) 5a²+3ab
(2) 50

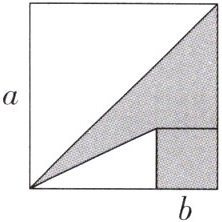
13.【教材P117习题T6变式】如图,已知两个正方形的边长分别为a,b,且$a+b= 10,ab= 18$,求阴影部分的面积.
]

答案： 由题意得，两个正方形边长分别为$a$和$b$。
阴影部分面积等于两个正方形面积之和减去两个空白三角形面积。
两个正方形面积之和为$a^{2}+b^{2}$。
大空白三角形面积为$\frac{1}{2}a^{2}$，小空白三角形面积为$\frac{1}{2}b(a + b)$。
则阴影部分面积$S=a^{2}+b^{2}-\frac{1}{2}a^{2}-\frac{1}{2}b(a + b)$
$=\frac{1}{2}a^{2}+\frac{1}{2}b^{2}-\frac{1}{2}ab$
$=\frac{1}{2}(a + b)^{2}-\frac{3}{2}ab$。
已知$a + b = 10$，$ab = 18$，代入上式得：
$S=\frac{1}{2}×10^{2}-\frac{3}{2}×18$
$=50 - 27$
$= 23$
所以阴影部分面积为$23$。

易错特训 计算$(-2x-y)^{2}$的结果是 ( )

A.$-4x^{2}-y^{2}$
B.$4x^{2}+y^{2}$
C.$4x^{2}+4xy+y^{2}$
D.$-4x^{2}-4xy-y^{2}$

答案： $(-2x - y)^2$
$= [-(2x + y)]^2$
$=(2x + y)^2$
$=(2x)^2 + 2 \cdot 2x \cdot y + y^2$
$=4x^2 + 4xy + y^2$
C