《2025年名校作业八年级数学上册人教版湖北专版》

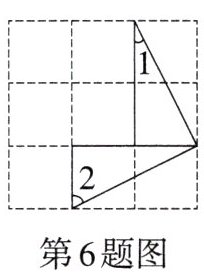
6.如图,在正方形网格中,三角形的顶点均在格点上,则∠1+∠2的度数为______。

答案： 连接格点构造三角形，设小正方形边长为1。
在网格中，取∠1所在的直角三角形，直角边分别为1和2；取∠2所在的直角三角形，直角边分别为1和2。
根据SAS判定，两直角三角形全等（直角边对应相等，夹角均为直角），故对应角相等。
将两三角形的直角边拼接，形成一个等腰直角三角形，其锐角为45°，即∠1+∠2=45°。
45°

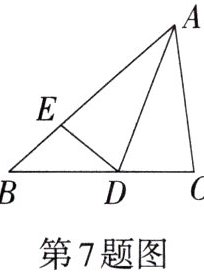
7.如图,在△ABC中,AB= 6,BC= 5,AC= 4,AD平分∠BAC交BC于点D,在AB上截取AE= AC,则△BDE的周长为______。

答案： 7

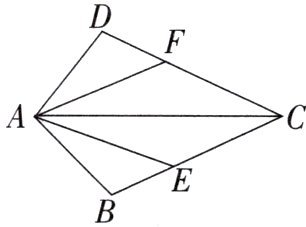
8.如图,AB= AD,CE= CF,AC是∠BAD的平分线。求证：AE= AF。

答案： 证明：
$\because AC$是$\angle BAD$的平分线。
$\therefore \angle BAC=\angle DAC$。
$\because$ 在$\triangle ABC$和$\triangle ADC$中，
$\begin{cases}AB=AD,\\\angle BAC=\angle DAC,\\AC=AC.\end{cases}$
$\therefore \triangle ABC\cong\triangle ADC(SAS)$。
$\therefore \angle BCA=\angle DCA$。
$\because$ 在$\triangle ACE$和$\triangle ACF$中，
$\begin{cases}CE=CF,\\\angle BCA=\angle DCA,\\AC=AC.\end{cases}$
$\therefore \triangle ACE\cong\triangle ACF(SAS)$。
$\therefore AE=AF$。

9.阅读下面材料：
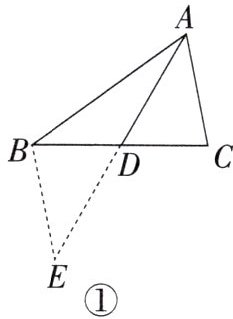
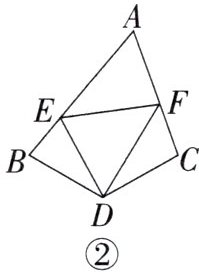
课外兴趣小组活动时,老师提出了如下问题：如图①,在△ABC中,AB= 5,AC= 3,求BC边上的中线AD的取值范围。
小明在小组内经过合作交流,得到了如下的解决方法：延长AD到点E,使ED= AD,再连接BE,就把AB,AC,2AD集中在△ABE中,利用三角形的三边关系,可得AE的取值范围,从而得到AD的取值范围。

请你解决以下问题：
(1)请你根据上述的解决方法求AD的取值范围。
(2)如图②,在四边形ABDC中,∠B+∠ACD= 180°,BD= CD,∠BDC= 120°,以点D为顶点作一个60°的角,角的两边分别交AB,AC于E,F两点,连接EF,探究线段BE,CF,EF之间的数量关系,并加以证明。

答案：
(1)1＜AD＜4；
(2)EF=BE+CF。