《2025年名校作业八年级数学上册人教版湖北专版》

1.【教材 P22 复习题 T9】如图,连接 AC,AD,BD,BE,CE,求证:∠A+∠B+∠C+∠D+∠E= 180°.

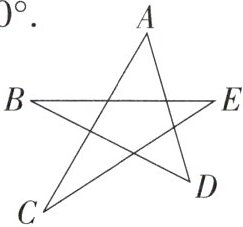
答案： 证明：设AC与BD交于点M，AD与CE交于点N。
∵∠AMD是△ABM的外角，
∴∠AMD=∠A+∠B（三角形的外角等于与它不相邻的两个内角的和）。
∵∠DNE是△CDN的外角，
∴∠DNE=∠C+∠D（同理）。
在△MNE中，∠NME+∠MNE+∠E=180°（三角形内角和定理）。
∵∠NME=∠AMD，∠MNE=∠DNE（对顶角相等），
∴∠AMD+∠DNE+∠E=180°。
∴（∠A+∠B）+（∠C+∠D）+∠E=180°，即∠A+∠B+∠C+∠D+∠E=180°。

2. 如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数为______.

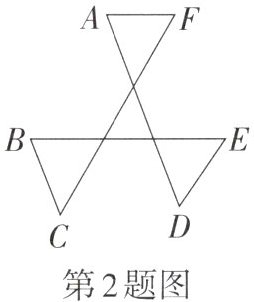
答案： 连接AF、BE、CD的交点为O（设交叉点为O）。
在△AOF中，∠A+∠F=180°-∠AOF；
在△BOC中，∠B+∠C=180°-∠BOC；
在△DOE中，∠D+∠E=180°-∠DOE。
∵∠AOF=∠DOE（对顶角相等），∠BOC=∠AOF（对顶角相等），设∠AOF=∠DOE=∠BOC=α，
又
∵∠AOF+∠BOC+∠DOE=3α=180°（平角定义），
∴α=60°。
∴∠A+∠B+∠C+∠D+∠E+∠F=(180°-α)+(180°-α)+(180°-α)=540°-3α=540°-180°=360°。
360°

3. 如图,∠A+∠B+∠C+∠D+∠E+∠F 的度数为______.

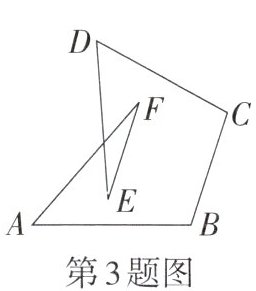
答案： 连接AD，设AF与DE交于点O。
在△AOE中，∠AEO+∠EAO=∠AOD（三角形外角等于不相邻两内角和）；
在△DOF中，∠DFO+∠FDO=∠AOD（同理）；
∴∠AEO+∠EAO=∠DFO+∠FDO，即∠E+∠FAD=∠F+∠EDA。
∠A+∠D=∠FAD+∠BAD+∠EDA+∠CDA=（∠FAD+∠EDA）+∠BAD+∠CDA=（∠E+∠F）+∠BAD+∠CDA。
在四边形ABCD中，∠BAD+∠B+∠C+∠CDA=360°（四边形内角和为360°，由两个三角形内角和得）。
∴∠A+∠B+∠C+∠D+∠E+∠F=（∠FAD+∠EDA+∠BAD+∠CDA）+∠B+∠C=（∠E+∠F+∠BAD+∠CDA）+∠B+∠C=∠BAD+∠B+∠C+∠CDA+∠E+∠F=360°。
360°

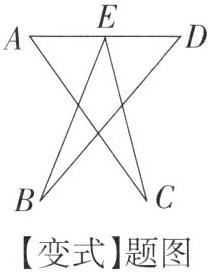
【变式】如图,∠A+∠B+∠C+∠D+∠E 的度数为______.

答案： 连接CD，设BD与CE交于点O。
在△BOE中，∠BOC是外角，
∴∠BOC=∠B+∠E。
在△COD中，∠BOC=∠OCD+∠ODC（三角形内角和定理的推论：三角形的一个外角等于和它不相邻的两个内角的和）。
∴∠B+∠E=∠OCD+∠ODC。
∠A+∠B+∠C+∠D+∠E=∠A+（∠B+∠E）+∠C+∠D=∠A+（∠OCD+∠ODC）+∠C+∠D=∠A+（∠OCD+∠C）+（∠ODC+∠D）=∠A+∠ACD+∠ADC。
在△ACD中，∠A+∠ACD+∠ADC=180°（三角形内角和定理）。
∴∠A+∠B+∠C+∠D+∠E=180°。
180°

4. 阅读下面材料,并完成相应的任务.
如图①,我们把四边形 ABDC 称为"箭头图",该图有这样一个性质:∠BDC= ∠A+∠B+∠C. 下面是该性质的证明过程.
证明:如图②,连接 AD 并延长到点 E. ∵∠1= ∠B+∠BAD(依据),∠2= ∠C+∠CAD,∴∠BDC= ∠1+∠2= ∠B+∠BAD+∠CAD+∠C,即∠BDC= ∠A+∠B+∠C.
任务:
(1)填空:材料中的"依据"是指______.
(2)你还能想出其他解法吗? 请写出解答过程.
(3)一个零件的形状如图③所示,按规定∠A 应等于 110°才合格,经检验,∠B= 18°,∠C= 20°,∠BDC= 145°,那么这个零件______. (填"合格"或"不合格")

答案：
(1) 三角形的外角等于与它不相邻的两个内角的和
(2) 延长BD交AC于点E。
∵∠BEC是△ABE的外角，
∴∠BEC=∠A+∠B（三角形的外角等于与它不相邻的两个内角的和）。
∵∠BDC是△DEC的外角，
∴∠BDC=∠BEC+∠C（三角形的外角等于与它不相邻的两个内角的和）。
∴∠BDC=∠A+∠B+∠C。
(3) 不合格