《2025年名校作业八年级数学上册人教版湖北专版》

7. 如图,∠3= 30°,为了使白球反弹后将黑球直接撞入袋口(∠1= ∠2),必须保证在击打白球时,∠1的度数为______.

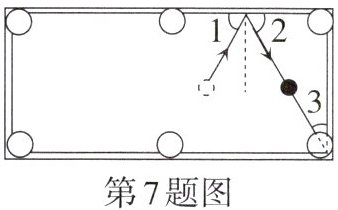
答案： $\because\angle 3=30^\circ$，台球桌四边互相平行，
$\therefore \angle 4=\angle 3=30^\circ$。
$\because \angle 1=\angle 2$，
$\therefore \angle 1+\angle 2+\angle 4=180^\circ-90^\circ=90^\circ$。
$\therefore 2\angle 1+30^\circ=90^\circ$。
$\therefore \angle 1=30^\circ$。
故答案为$30^\circ$。

8. 如图,在Rt△ACB中,∠BAC= 90°,AD⊥BC,垂足为点D,△ABD与△AB'D关于直线AD对称,点B的对称点是点B'.若∠B'AC= 14°,则∠B的度数为______.

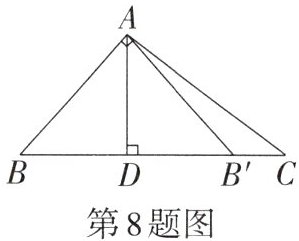
答案：
∵△ABD与△AB'D关于直线AD对称，
∴∠BAD=∠B'AD。
设∠B=α，在Rt△ABC中，∠BAC=90°，
∴∠C=90°-α。
∵AD⊥BC，
∴∠ADB=90°，在Rt△ABD中，∠BAD=90°-∠B=90°-α，故∠B'AD=90°-α。
在Rt△ADC中，∠DAC=90°-∠C=α（
∵∠C=90°-α）。
∵∠DAC=∠B'AD+∠B'AC，∠B'AC=14°，
∴α=(90°-α)+14°。
解得2α=104°，α=52°。
∠B=52°
52°

9. 如图,在△ABC中,点D在BC边上,点D关于AB,AC的对称点分别为点E,F,连接AE,AF.若∠B= 61°,∠C= 54°,则∠EAF的度数为______.

答案： 130°

10. 如图,直线l,m相交于点O,P是这两条直线外一点,且OP= 2.8,点P关于直线l,m的对称点分别是点$P_1,P_2,$则$P_1,P_2$之间的距离d的取值范围为______.

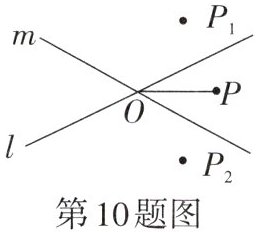
答案： 连接OP₁，OP₂。
∵P₁是P关于直线l的对称点，
∴OP₁=OP=2.8。
∵P₂是P关于直线m的对称点，
∴OP₂=OP=2.8。
设直线l与m的夹角为α（0°＜α＜180°），则∠P₁OP₂=2α（0°＜2α＜360°，取0°＜∠P₁OP₂＜180°）。
在△P₁OP₂中，由三角形三边关系：
当∠P₁OP₂=0°时，P₁P₂=|OP₁-OP₂|=0（取不到）；
当∠P₁OP₂=180°时，P₁P₂=OP₁+OP₂=5.6（取不到）。
∴d的取值范围为0＜d＜5.6。
0＜d＜5.6

11. 如图是由边长均为1的小正方形组成的网格,并且都已经填充了一部分阴影,请按下列要求对图形用阴影进行填充.
(1)使图①成为轴对称图形;
(2)使图②成为有4条对称轴且阴影部分面积等于3的图形;
(3)使图③成为有2条对称轴且阴影部分面积不超过6的图形.

答案： （1）在图①中，沿着正方形对边中点连线对折后，已填充阴影部分关于这条直线对称，在已填充阴影部分关于对边中点连线对称的位置，填充阴影，使图①成为轴对称图形（答案不唯一）。
（2）图②中，正方形有$4$条对称轴，分别是两条对角线所在的直线和过对边中点的直线。
已填充阴影部分是一个直角边为$1$的等腰直角三角形，面积为$\frac{1}{2}×1×1 = \frac{1}{2}$。
要使阴影部分面积为$3$，可以在已填充阴影部分关于$4$条对称轴对称的位置，分别填充阴影。
例如，以正方形的两条对角线以及两组对边中点连线为对称轴，在相应对称位置填充阴影，使得阴影部分由$6$个上述等腰直角三角形组成，面积为$6×\frac{1}{2}=3$。
（3）图③中，可以以正方形的两条对角线为对称轴。
已填充阴影部分是一个直角边分别为$1$和$2$的直角三角形，面积为$\frac{1}{2}×1×2 = 1$。
在已填充阴影部分关于两条对角线对称的位置，分别填充阴影，使得阴影部分由$4$个上述直角三角形和$2$个边长为$1$的正方形组成，面积为$4×1 + 2×1×1= 6$，满足有$2$条对称轴且阴影部分面积不超过$6$。

12. 如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处.
(1)求证:△GCF≌△BCE.
(2)若CD= 8,BC= 4,求四边形ECGF的面积.

答案：
(1)见证明过程；
(2)16。