《2025年名校作业八年级数学上册人教版湖北专版》

1.【教材 P118 习题 T7】已知$a+b= 5$,$ab= 3$,求$a^{2}+b^{2}$的值.

答案： 答题卡：
解：
已知 $a + b = 5$，$ab = 3$，
根据完全平方公式，我们有
$(a + b)^{2} = a^{2} + 2ab + b^{2}$
将 $a + b = 5$ 代入上式，得
$5^{2} = a^{2} + 2ab + b^{2}$
即
$25 = a^{2} + 2ab + b^{2}$
再将 $ab = 3$ 代入上式，得
$25 = a^{2} + 2 × 3 + b^{2}$
即
$25 = a^{2} + 6 + b^{2}$
从上式解出 $a^{2} + b^{2}$，得
$a^{2} + b^{2} = 25 - 6 = 19$
故答案为：$a^{2} + b^{2} = 19$。

类型 1 $a^{2}+b^{2}$的变形

答案： 题目：已知$a + b = 5$，$ab = 3$，求$a^2 + b^2$的值。
解答：
根据完全平方公式，有
$(a+b)^2 = a^2 + 2ab + b^2$，
移项得
$a^2 + b^2 = (a+b)^2 - 2ab$，
将$a + b = 5$和$ab = 3$代入上式，得
$a^2 + b^2 = 5^2 - 2 × 3 = 25 - 6 = 19$。
所以，$a^2 + b^2 = 19$。

2. 已知$a-b= 10$,$ab= 5$,则$a^{2}+b^{2}= $______.

答案： 答题卡：
解：
∵ $a - b = 10$，$ab = 5$，
∴ $a^{2} + b^{2} = (a - b)^{2} + 2ab$
$= 10^{2} + 2 × 5$
$= 100 + 10$
$= 110$
故答案为：$110$。

3. 已知$m$,$n满足(m+n)^{2}= 169$,$(m-n)^{2}= 9$,则$m^{2}+n^{2}= $______.

答案： 答题卡：
3.
由完全平方公式，我们有：
$(m+n)^{2} = m^{2} + 2mn + n^{2}$
$(m-n)^{2} = m^{2} - 2mn + n^{2}$
根据题意，$(m+n)^{2} = 169$，所以 $m^{2} + 2mn + n^{2} = 169$ ①
同样，$(m-n)^{2} = 9$，所以 $m^{2} - 2mn + n^{2} = 9$ ②
将①和②两式相加，得到：
$2m^{2} + 2n^{2} = 178$
从中我们可以得出：
$m^{2} + n^{2} = 89$
故答案为：89。

4. 若$(2-x)(x-3)= -5$,则$(2-x)^{2}+(x-3)^{2}$的值为______.

答案： 设$a = 2 - x$，$b = x - 3$，则$ab=-5$。
计算$a + b$：$a + b=(2 - x)+(x - 3)=-1$。
由完全平方公式变形得：$a^2 + b^2=(a + b)^2-2ab$。
代入$a + b=-1$，$ab=-5$：$a^2 + b^2=(-1)^2-2×(-5)=1 + 10=11$。
故$(2 - x)^2+(x - 3)^2=11$。
11

类型 2 $ab$的变形

答案： 答案略

5. 若$a+b= 14$,$a^{2}+b^{2}= 100$,则$ab= $______.

答案： 答题卡：
解：
∵$(a+b)^{2} = a^{2} + 2ab + b^{2}$，
∴$2ab = (a+b)^{2} - (a^{2} + b^{2})$，
代入已知条件 $a+b=14$ 和 $a^{2}+b^{2}=100$，
得 $2ab = 14^{2} - 100 = 196 - 100 = 96$，
∴$ab = \frac{96}{2} = 48$。
故答案为：$48$。

6. 若$a^{2}+b^{2}= 5$,$a-b= 3$,则$ab= $______.

答案： $-2$

7. 若$(a+b)^{2}= 16$,$(a-b)^{2}= 4$,则$ab= $______.

答案： 答题卡：
7.
∵ $(a+b)^{2} = a^{2} + 2ab + b^{2} = 16$，
$(a-b)^{2} = a^{2} - 2ab + b^{2} = 4$，
∴ $a^{2} + 2ab + b^{2} - (a^{2} - 2ab + b^{2}) = 16 - 4$，
即 $4ab = 12$，
∴ $ab = 3$。
故答案为：$3$。

类型 3 $(a\pm b)^{2}$的变形

答案： 假设题目为：已知$a + b = 5$，$ab = 3$，求$a^2 + b^2$和$(a - b)^2$的值。
答题卡：
解：
1. 求$a^2 + b^2$：
根据完全平方公式，有
$(a + b)^2 = a^2 + 2ab + b^2$
移项得
$a^2 + b^2 = (a + b)^2 - 2ab$
代入已知条件$a + b = 5$和$ab = 3$，得
$a^2 + b^2 = 5^2 - 2 × 3 = 25 - 6 = 19$
2. 求$(a - b)^2$：
根据完全平方公式，有
$(a - b)^2 = a^2 - 2ab + b^2$
这也可以表示为
$(a - b)^2 = (a + b)^2 - 4ab$
代入已知条件$a + b = 5$和$ab = 3$，得
$(a - b)^2 = 5^2 - 4 × 3 = 25 - 12 = 13$
综上，$a^2 + b^2 = 19$，$(a - b)^2 = 13$。

8.【例题呈现】已知$a+b= 5$,$ab= 3$,求$(a-b)^{2}$的值.

答案： 答题卡：
解：
根据完全平方公式，我们有
$(a-b)^{2} = a^{2} - 2ab + b^{2}$
又因为
$(a+b)^{2} = a^{2} + 2ab + b^{2}$
所以
$(a-b)^{2} = (a+b)^{2} - 4ab$
代入已知条件 $a+b=5$ 和 $ab=3$，得
$(a-b)^{2} = 5^{2} - 4 × 3 = 25 - 12 = 13$
故 $(a-b)^{2}$ 的值为 13。

【方法探究】(1)请将方法二补充完整.
| 方法一 | 方法二 |
| :----------------------------------------------------------- | :----------------------------------------------------------- |
| $\because (a+b)^{2}= a^{2}+2ab+b^{2}$,$a+b= 5$,$ab= 3$,$\therefore a^{2}+b^{2}= (a+b)^{2}-2ab= 5^{2}-2×3= 19$.$\therefore (a-b)^{2}= a^{2}+b^{2}-2ab= 19-2×3= 13$. | $\because (a+b)^{2}= a^{2}+2ab+b^{2}$,$(a-b)^{2}= a^{2}-2ab+b^{2}$,$\therefore (a-b)^{2}= (a+b)^{2}-$______.$\because a+b= 5$,$ab= 3$,$\therefore (a-b)^{2}= 5^{2}-4×3= 13$. |

答案： 4ab

【拓展提升】(2)如图,分别以 Rt△ABC 的直角边 AB,BC 为边作正方形 ABDE 和正方形 BCFG. 若△ABC 的面积为 5,正方形 ABDE 和正方形 BCFG 的面积之和为 36,求 AG 的长.

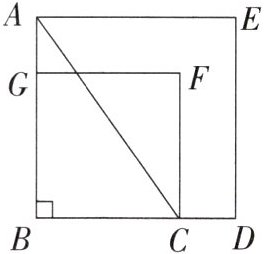
答案： 4