第77页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
【问题提出】
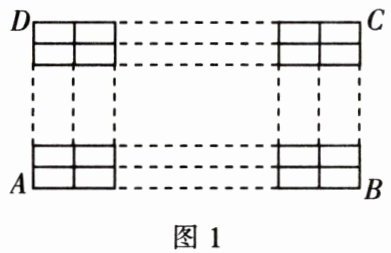
将长方形$ABCD的四条边都n (n \geq 2)$等分,分别连接长方形$ABCD$对边的各对应的等分点,得到如图1所示的图形,探究图1中共有多少个长方形。(包括图中所有的长方形)
【问题探究】
为解决上面的问题,小李采取一般问题特殊化的策略。她先从最简单的二等分入手开始探究,再依据积累的解题经验,逐渐深入,最后探究【问题提出】中的问题。下面是小李探究的过程:
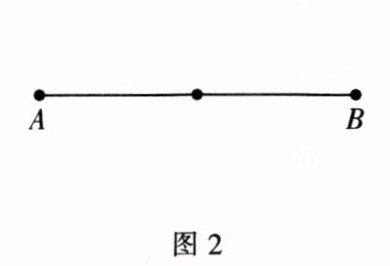
如图2,小李先将$AB$边二等分,则等分点将$AB边分为\frac{1}{2} × 2 × 3$条线段,即3条线段;
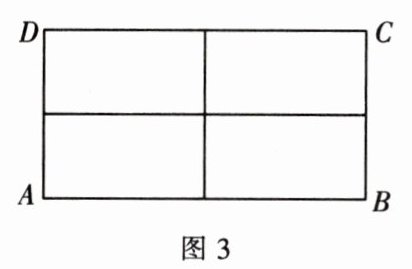
接着按照上述方法将其他三边$BC$,$CD$,$AD$分别二等分,连接$AB$,$CD$对边各对应等分点,再连接$BC$,$AD$对边各对应等分点,进而得到如图3所示的图形,于是小李发现,图3中共有长方形的个数为$(\frac{1}{2} × 2 × 3) × (\frac{1}{2} × 2 × 3) = (\frac{1}{2} × 2 × 3)^2 = 3^2 = 9$。
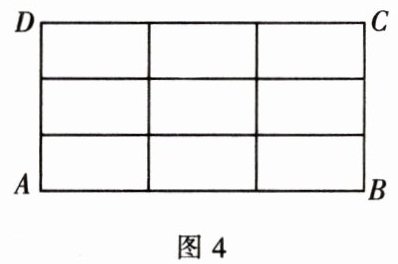
小李继续按上述二等分的方法,将长方形$ABCD的边AB$,$BC$,$CD$,$AD$分别三等分,再连接对边各对应的等分点得到如图4所示的图形,于是小李发现,图4中共有长方形的个数为$(\frac{1}{2} × 3 × 4) × (\frac{1}{2} × 3 × 4) = (\frac{1}{2} × 3 × 4)^2 = 6^2 = 36$。
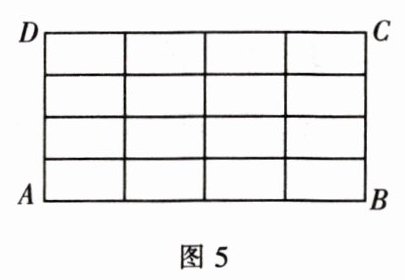
(1) 如图5是小李继续按照上述探究方法得到的图形,请你依据小李的探究经验,求出图5中共有多少个长方形。
【问题解决】
(2) 依据上述的解题经验,请你求出【问题提出】中的图1共有多少个长方形。
【拓展延伸】
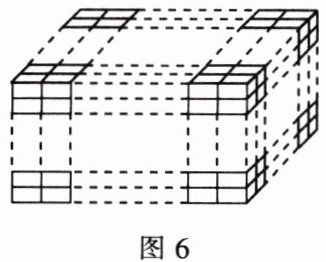
(3) 将一个长方体的各条棱$n (n \geq 2)$等分,连接各条棱上对应的等分点得到如图6所示的图形,请求出图6中共有多少个长方体。(包括图中所有的长方体)
将长方形$ABCD的四条边都n (n \geq 2)$等分,分别连接长方形$ABCD$对边的各对应的等分点,得到如图1所示的图形,探究图1中共有多少个长方形。(包括图中所有的长方形)
【问题探究】
为解决上面的问题,小李采取一般问题特殊化的策略。她先从最简单的二等分入手开始探究,再依据积累的解题经验,逐渐深入,最后探究【问题提出】中的问题。下面是小李探究的过程:
如图2,小李先将$AB$边二等分,则等分点将$AB边分为\frac{1}{2} × 2 × 3$条线段,即3条线段;
接着按照上述方法将其他三边$BC$,$CD$,$AD$分别二等分,连接$AB$,$CD$对边各对应等分点,再连接$BC$,$AD$对边各对应等分点,进而得到如图3所示的图形,于是小李发现,图3中共有长方形的个数为$(\frac{1}{2} × 2 × 3) × (\frac{1}{2} × 2 × 3) = (\frac{1}{2} × 2 × 3)^2 = 3^2 = 9$。
小李继续按上述二等分的方法,将长方形$ABCD的边AB$,$BC$,$CD$,$AD$分别三等分,再连接对边各对应的等分点得到如图4所示的图形,于是小李发现,图4中共有长方形的个数为$(\frac{1}{2} × 3 × 4) × (\frac{1}{2} × 3 × 4) = (\frac{1}{2} × 3 × 4)^2 = 6^2 = 36$。
(1) 如图5是小李继续按照上述探究方法得到的图形,请你依据小李的探究经验,求出图5中共有多少个长方形。






【问题解决】
(2) 依据上述的解题经验,请你求出【问题提出】中的图1共有多少个长方形。
【拓展延伸】
(3) 将一个长方体的各条棱$n (n \geq 2)$等分,连接各条棱上对应的等分点得到如图6所示的图形,请求出图6中共有多少个长方体。(包括图中所有的长方体)
答案:
解:(1)$\left(\dfrac{1}{2}× 4× 5\right)× \left(\dfrac{1}{2}× 4× 5\right)=\left(\dfrac{1}{2}× 4× 5\right)^2=10^2=100$。(2)$\dfrac{1}{2}n(n+1)× \dfrac{1}{2}n(n+1)=\left[\dfrac{1}{2}n(n+1)\right]^2$。(3)$\dfrac{1}{2}n(n+1)× \dfrac{1}{2}n(n+1)× \dfrac{1}{2}n(n+1)=\left[\dfrac{1}{2}n(n+1)\right]^3$。
查看更多完整答案,请扫码查看


