《2025年新课程能力培养七年级数学上册北师大版》

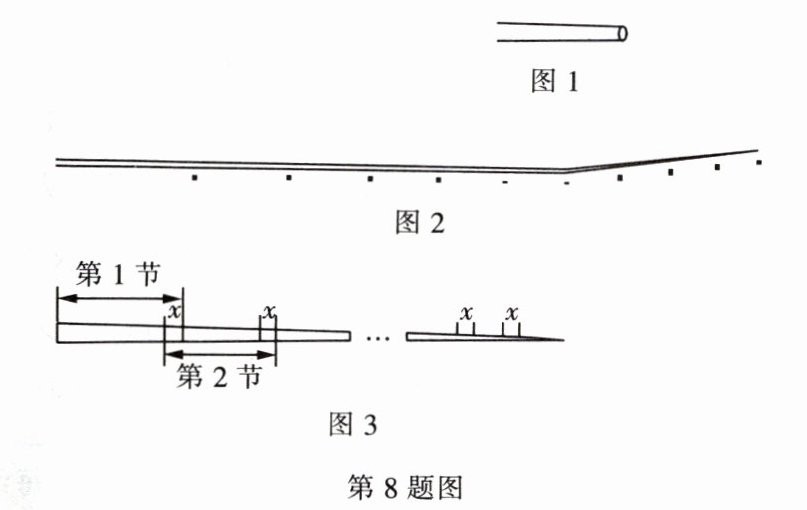
8. 如图是一根可伸缩的鱼竿,鱼竿是用10节大小不同的空心套管连接而成的。闲置时鱼竿可收缩,完全收缩后,鱼竿长度即为第1节套管的长度(如图1所示),使用时,可将鱼竿的每一节套管都完全拉伸(如图2所示)。图3是这根鱼竿所有套管都处于完全拉伸状态下的平面示意图。已知第1节套管长50cm,第2节套管长46cm,依次类推,每一节套管均比前一节套管短4cm。完全拉伸时,为了使相邻两节套管连接并固定,每相邻两节套管间均有相同长度的重叠,设其长度为x cm。
(1)请直接写出第5节套管的长度。
(2)当这根鱼竿完全拉伸时,其长度为311cm,求x的值。

答案： （1）第5节套管的长度为 $ 50-4×(5-1)=34 $（cm）。（2）第10节套管的长度为 $ 50-4×(10-1)=14 $（cm）。设每相邻两节套管间重叠的长度为 $ x\ cm $，根据题意，得 $ (50+46+42+\cdots+14)-9x=311 $，即 $ 320-9x=311 $。解得 $ x=1 $。答：每相邻两节套管间重叠的长度为 1 cm。

9. (2022·绥化)在长为2、宽为x(1 ＜ x ＜ 2)的矩形纸片上,从它的一侧剪去一个以矩形纸片宽为边长的正方形(第一次操作)；从剩下的矩形纸片一侧再剪去一个以宽为边长的正方形(第二次操作)；按此方式,如果第三次操作后,剩下的纸片恰为正方形,则x的值为______。

答案： 1.2 或 1.5 提示：第一次操作后的两边长分别是 $ x $ 和 $ (2-x) $，$ \because 1＜x＜2 $，$ \therefore x＞2-x $，$ \therefore $ 第二次操作后的两边长分别是 $ (2x-2) $ 和 $ (2-x) $。当 $ 2x-2＞2-x $ 时，有 $ 2x-2=2(2-x) $，解得 $ x=1.5 $；当 $ 2x-2＜2-x $ 时，有 $ 2(2x-2)=2-x $，解得 $ x=1.2 $。

10. (2024·宿迁)我国古代问题：以绳测井,若将绳三折测之,绳多四尺；若将绳四折测之,绳多一尺。绳长、井深各几何？这段话的意思是：用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺。绳长、井深各几尺？若设绳长为x尺,则可列方程为( )

A.$\frac{1}{3}x - 4 = \frac{1}{4}x - 1$
B.$\frac{1}{3}x + 4 = \frac{1}{4}x - 1$
C.$\frac{1}{3}x - 4 = \frac{1}{4}x + 1$
D.$\frac{1}{3}x + 4 = \frac{1}{4}x + 1$

答案： A

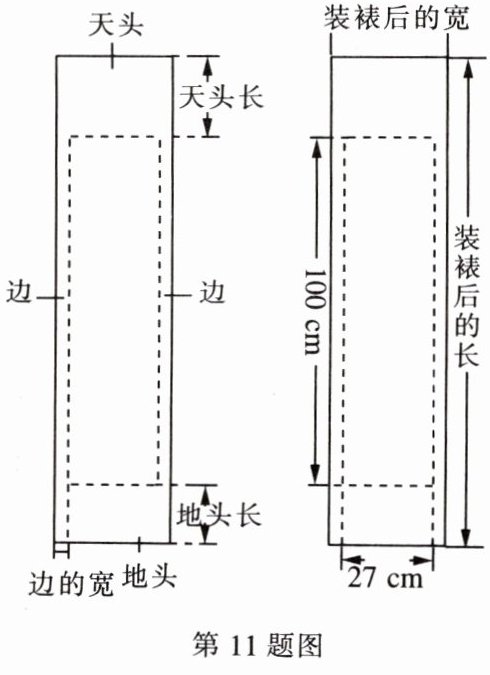
11. (2023·北京)对联是中华传统文化的瑰宝,对联装裱后如图所示,上、下空白处分别称为天头和地头,左、右空白处统称为边。一般情况下,天头长与地头长的比是6:4,左、右边的宽相等,均为天头长与地头长的和的$\frac{1}{10}$。某人要装裱一副对联,对联的长为100cm,宽为27cm。若要求装裱后的长是装裱后的宽的4倍,求边的宽和天头长。

答案： 解：设天头长为 $ 6x\ cm $，地头长为 $ 4x\ cm $，则左、右边的宽为 $ x\ cm $。根据等量关系，列出方程，得 $ 100+(6x+4x)=4×(27+2x) $。解这个方程，得 $ x=4 $。进而 $ 6x=24 $。因此，边的宽为 4 cm，天头长为 24 cm。