第2页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
2. 写出下列立体图形的名称。


答案:
(1)圆柱 (2)长方体 (3)圆锥 (4)四棱柱 (5)三棱柱
3. 按围成立体图形的各个面中是否有曲面划分,与圆柱为同一类几何体的是( )
A.圆锥
B.长方体
C.正方体
D.棱柱
A.圆锥
B.长方体
C.正方体
D.棱柱
答案:
A
4. 八棱柱的顶点数、棱数和面数分别是( )
A.16,10,24
B.8,24,10
C.16,24,10
D.10,16,24
A.16,10,24
B.8,24,10
C.16,24,10
D.10,16,24
答案:
C
5. 请将以下物体和与其形状类似的几何体用线连起来。
①篮球 ②魔方 ③砖块 ④烟囱帽 ⑤易拉罐
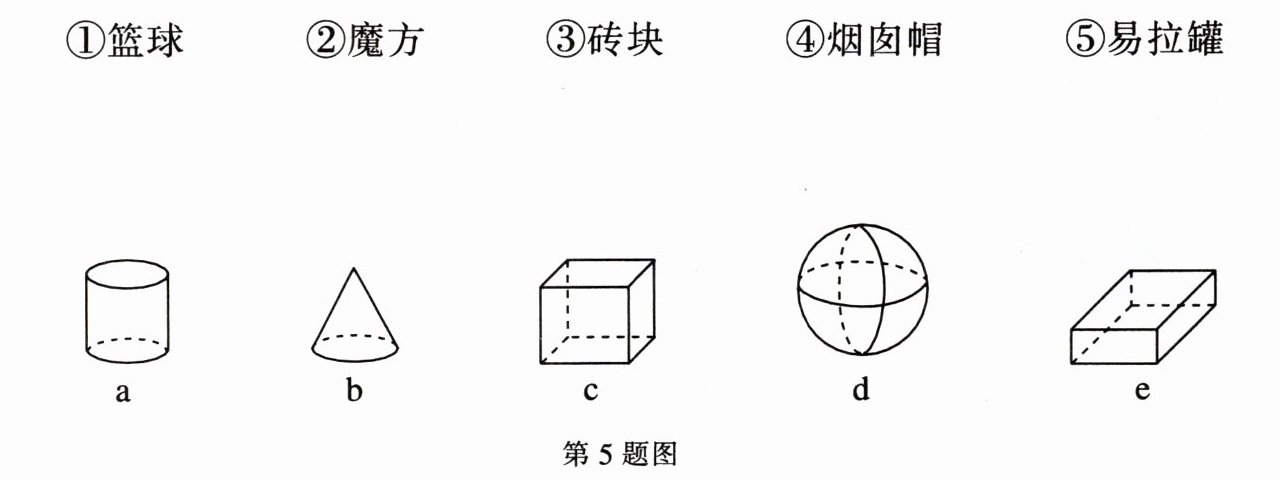
①篮球 ②魔方 ③砖块 ④烟囱帽 ⑤易拉罐

答案:
①—d ②—c ③—e ④—b ⑤—a
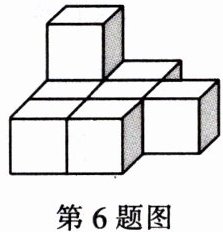
6. 如图是由若干个小立方块堆成的立体图形,在这个基础上要把它堆成一个大立方块,至少还需要多少个同样大的小立方块?为什么?

答案:
解:至少还需要19个。理由:堆成大立方块至少共需要小立方块$3^{3}$个,即27个,现在这个几何体中有8个小立方块,所以至少还需要27-8=19(个)。
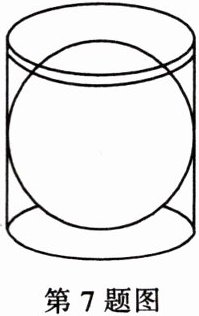
7. (2024·大庆)如图所示,一个球恰好放在一个圆柱形容器里,记球的体积为$V_1$,圆柱形容器的容积为$V_2$,则$\frac{V_1}{V_2}= $______。(球体积公式:$V = \frac{4}{3}\pi r^3$,其中r为球半径)

答案:
$\frac{2}{3}$
查看更多完整答案,请扫码查看


