第95页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
10. 如图,这是由截面为同一种长方形的墙砖粘贴的部分墙面,其中三块横放的墙砖比两块竖放的墙砖低$30\ cm$,两块竖放的墙砖比两块横放的墙砖高$50\ cm$,则每块墙砖的截面面积是
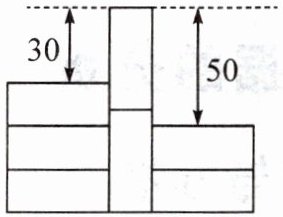
900
$cm^{2}$.
答案:
10.900
11. 请用二元一次方程组解决问题:
某校八年级(1)班和(2)班的学生一块到航天科普教育基地进行社会大课堂活动,两班学生共$104$人,其中(1)班学生比(2)班学生少,教育基地门票价格如下:

原计划两班都以班为单位购票,则一共应付$1136$元.请回答下列问题:
(1)八年级(1)班有多少人?
(2)作为组织者,应如何购票最省钱? 比原计划节省多少钱?
某校八年级(1)班和(2)班的学生一块到航天科普教育基地进行社会大课堂活动,两班学生共$104$人,其中(1)班学生比(2)班学生少,教育基地门票价格如下:

原计划两班都以班为单位购票,则一共应付$1136$元.请回答下列问题:
(1)八年级(1)班有多少人?
(2)作为组织者,应如何购票最省钱? 比原计划节省多少钱?
答案:
11.解:
(1)设八年级
(1)班有$x$人,八年级
(2)班有$y$人。$\because x < y$,$\therefore y > 52$.$①$当$x = 51,y = 53$时,$10(x + y) = 10 × 104 = 1040 \neq 1136$,不符合题意;$②$当$x \leq 50$时,则$\begin{cases} x + y = 104, \\ 12x + 10y = 1136 \end{cases}$,解得$\begin{cases} x = 48, \\ y = 56 \end{cases}$.或$\begin{cases} x + y = 104, \\ 12x + 8y = 1136 \end{cases}$,解得$\begin{cases} x = 76, \\ y = 28 \end{cases}$(舍去)。答:八年级
(1)班有48人。
(2)两个班一起购票最省钱。比原计划节省$1136 - 8 × 104 = 1136 - 832 = 304(元)$。
(1)设八年级
(1)班有$x$人,八年级
(2)班有$y$人。$\because x < y$,$\therefore y > 52$.$①$当$x = 51,y = 53$时,$10(x + y) = 10 × 104 = 1040 \neq 1136$,不符合题意;$②$当$x \leq 50$时,则$\begin{cases} x + y = 104, \\ 12x + 10y = 1136 \end{cases}$,解得$\begin{cases} x = 48, \\ y = 56 \end{cases}$.或$\begin{cases} x + y = 104, \\ 12x + 8y = 1136 \end{cases}$,解得$\begin{cases} x = 76, \\ y = 28 \end{cases}$(舍去)。答:八年级
(1)班有48人。
(2)两个班一起购票最省钱。比原计划节省$1136 - 8 × 104 = 1136 - 832 = 304(元)$。
12. (2024·内蒙古)点$P(x,y)$在直线$y = - \frac{3}{4}x + 4$上,坐标$(x,y)$是二元一次方程$5x - 6y = 33$的解,则点$P$的位置在(
A.第一象限
B.第二象限
C.第三象限
D.第四象限
D
)A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
12.D
13. 甲、乙两人参加从$A$地到$B$地的长跑比赛,两人在比赛时所跑的路程$y$(米)与时间$x$(分)之间的函数关系如图所示,请根据图象,回答下列问题:
(1)
(2)根据图象,求出甲的函数表达式.
(3)甲、乙何时相遇?
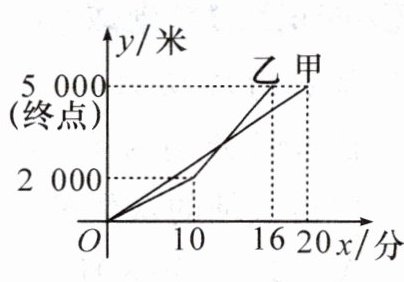
(1)
乙
先到达终点(填“甲”或“乙”).(2)根据图象,求出甲的函数表达式.
(3)甲、乙何时相遇?

答案:
13.解:
(1)乙
(2)设甲跑的路程$y$(米)与时间$x$(分)之间的关系式为$y = ax$,则$20a = 5000$,解得$a = 250.\therefore$甲的函数表达式为$y = 250x(0 \leq x \leq 20)$。
(3)当$10 \leq x \leq 16$时,设乙跑的路程$y$(米)与时间$x$(分)之间的关系式$y = kx + b$.将$(10,2000)$,$(16,5000)$代入,得$\begin{cases} 10k + b = 2000, \\ 16k + b = 5000 \end{cases}$,解得$\begin{cases} k = 500, \\ b = -3000 \end{cases}.\therefore y = 500x - 3000$.联立$\begin{cases} y = 250x, \\ y = 500x - 3000 \end{cases}$,解得$\begin{cases} x = 12, \\ y = 3000 \end{cases}.\therefore$甲与乙在12分钟时相遇。
(1)乙
(2)设甲跑的路程$y$(米)与时间$x$(分)之间的关系式为$y = ax$,则$20a = 5000$,解得$a = 250.\therefore$甲的函数表达式为$y = 250x(0 \leq x \leq 20)$。
(3)当$10 \leq x \leq 16$时,设乙跑的路程$y$(米)与时间$x$(分)之间的关系式$y = kx + b$.将$(10,2000)$,$(16,5000)$代入,得$\begin{cases} 10k + b = 2000, \\ 16k + b = 5000 \end{cases}$,解得$\begin{cases} k = 500, \\ b = -3000 \end{cases}.\therefore y = 500x - 3000$.联立$\begin{cases} y = 250x, \\ y = 500x - 3000 \end{cases}$,解得$\begin{cases} x = 12, \\ y = 3000 \end{cases}.\therefore$甲与乙在12分钟时相遇。
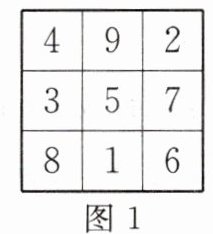
14. 新考向 数学文化 幻方是古老的数学问题,我国古代的《洛书》中记载了最早的幻方——九宫格.将$9$个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的$3$个数之和相等,例如图$1$就是一个幻方.若图$2$是一个未完成的幻方,则其中$x$与$y$的和是(
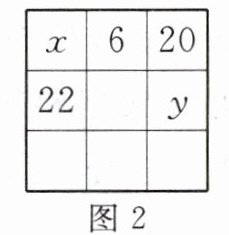
A.$9$
B.$10$
C.$11$
D.$12$
D
)

A.$9$
B.$10$
C.$11$
D.$12$
答案:
14.D
查看更多完整答案,请扫码查看


