《2025年名校课堂八年级数学上册北师大版内蒙古专版》

7. 两个正数的和是$24$，求它们积的最大值. 你有哪些解决问题的方法？

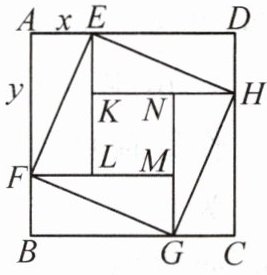
解：方法一：面积法(借助赵爽弦图).
设这两个正数分别为$x$，$y$，如图，用$8$个全等的直角边长分别为$x$，$y$的直角三角形拼成“弦图”.
由图可知$AE = DH = BF = CG = x$，$DE = AF = BG = CH = y$.
由题意，得$x + y=$24.
$8$个直角三角形的面积为$4xy=$S正方形ABCD$-S_{正方形KLMN}=$576$-S_{正方形KLMN}$，
$\therefore xy=$144$-\frac{1}{4}S_{正方形KLMN}$.
$\therefore$求$xy$的最大值，即求$S_{正方形KLMN}$的最小值.
又$\because S_{正方形KLMN}$最小值为0，
$\therefore xy$的最大值为144.
方法二：利用平方差公式求解.
设这两个正数分别为$12 - n$，12+n.
则它们的乘积为$(12 - n)\cdot$(12+n)$=$144$-n^{2}$.
$\therefore$求它们积的最大值，即求$n^{2}$的最小值.
又$\because n^{2}$的最小值为0，
$\therefore$它们积的最大值为144.

答案： 7.方法一：24；S正方形ABCD；576；144；0；144.方法二：12+n；(12+n)；144；0；144

8. 追本溯源：题（1）来自课本中的习题改编，请你完成解答，提炼方法并完成题（2）.
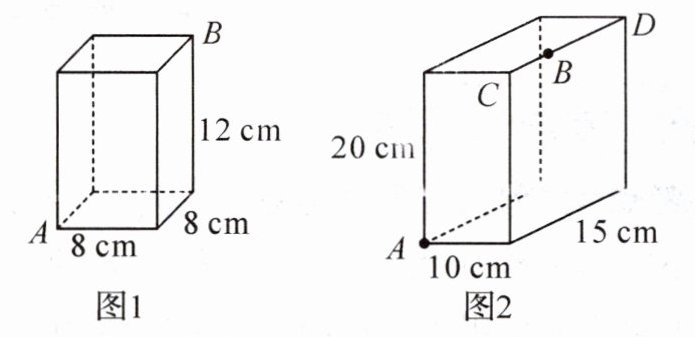
（1）如图$1$，一个长方体盒子，它的长、宽、高分别为$8cm$，$8cm$，$12cm$，一只蚂蚁想从盒底的点$A$沿盒的表面爬到盒顶的点$B$，你能帮蚂蚁设计一条最短的路线吗？蚂蚁要爬行的最短路程是多少？
（2）如图$2$，长方体的长为$15cm$，宽为$10cm$，高为$20cm$，点$B$在棱$CD$上，$CB = 5cm$，一只蚂蚁要沿长方体的表面从点$A$爬到点$B$，需要爬行的最短路程是多少？

答案： 8.（1）蚂蚁爬行的最短路线为A−P−B(P为CD的中点)，最短路程是20cm.（2）一只蚂蚁要沿长方体的表面从点A爬到点B，需要爬行的最短路程是25cm.