《2025年名校课堂八年级数学上册北师大版内蒙古专版》

9. 中国茶文化博大精深，祁门红茶在国内外享有盛誉，并被评为“中华十大名茶”。泡茶时，水温很有讲究。兰兰同学在煮茶时发现在一定时间内，水温 $ T ( ^ { \circ } C ) $是时间 $ t ( min ) $的一次函数，并且时间每增加 2 min，温度就升高 $ 16 ^ { \circ } C $。某次兰兰用 $ 18 ^ { \circ } C $的水温开始煮茶，设水温 $ T ( ^ { \circ } C ) $与时间 $ t ( min ) $之间的关系式为 $ T = kt + b $。
(1) 写出 $ T $ 与 $ t $ 之间的关系式为T=8t+18。
(2) $ k $ 的实际意义为每分钟水温的变化量，$ b $ 的实际意义为刚开始煮茶时水的温度。

答案： 9.
(1)T=8t+18
(2)每分钟水温的变化量 刚开始煮茶时水的温度

10. 若函数 $ y = ( m - 1 ) x ^ { m ^ { 2 } } + 3 $是关于 $ x $ 的一次函数，则 $ m $ 的值为-1。

答案： 10.-1

11.(本课时 T10 变式)已知 $ y = ( k - 1 ) x + k ^ { 2 } - 1 $，若 $ y $ 是 $ x $ 的正比例函数，则 $ k $ 的值为-1。

答案： 11.-1

12. 某校开展了主题为“生活中的一次函数”的项目学习，同学们找到了许多生活中的函数。下面实例中，变量之间的关系不是一次函数的是(B)

A.家庭用水的价格为 2.5 元/ $ m ^ { 3 } $，每月的水费支出与用水量之间的关系
B.百米赛跑中，时间与速度之间的关系
C.相同规格的 A4 纸整齐叠放，纸的厚度与纸的张数之间的关系
D.普通钟表指针转动的角度与所用时间的关系

答案： 12.B

13.（教材 P82 新增例 2 变式）“元旦”假期，小名和家人一起开车从家出发到距家 300 千米的邓小平故里旅游。已知小名家有两辆车（出发前油箱均已加满，假设行驶过程中汽车的耗油量均匀），混动车的剩余油量 $ Q _ { 1 } $（升）与行驶路程 $ x $（千米）之间的关系式为 $ Q _ { 1 } = 50 - 0.05x $，燃油车的剩余油量 $ Q _ { 2 } $（升）与行驶路程 $ x $（千米）之间的关系式为 $ Q _ { 2 } = 55 - 0.1x $。回答下列问题：
(1) 说明 $ Q _ { 1 } $中 0.05 的实际意义，并说明哪辆车的油箱更大。
(2) 当汽车到达邓小平故里时，求剩余油量 $ Q _ { 1 } $，$ Q _ { 2 } $的值。
(3) 当油箱中油量不超过 4 升时，汽车仪表盘油灯将自动报警，则当油灯刚好自动报警时，混动车比燃油车多行驶多少千米？

答案： 13.解：
(1)0.05表示混动车每千米的耗油量为0.05升，燃油车油箱容量为55升，混动车油箱容量为50升，所以燃油车油箱更大.
(2)当x=300时，Q₁=50-0.05x=50-0.05×300=35；Q₂=55-0.1x=55-0.1×300=25.
(3)当Q₁=Q₂=4时，4=50-0.05x₁，解得x₁=920.4=55-0.1x₂，解得x₂=510.920-510=410(千米).
∴当油灯刚好自动报警时，混动车比燃油车多行驶410千米。

14.(教材 P86 新增习题 T2 变式)将“$□$”和“$\triangle$”按如图所示的方式有规律的排列。
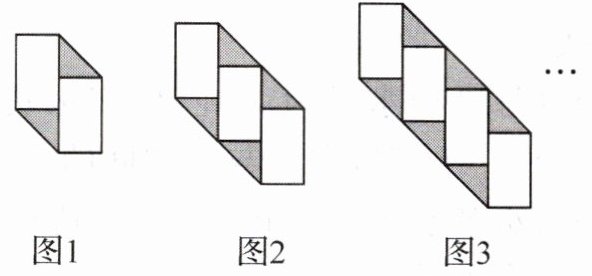
(1) 设图 $ n $ 中“$□$”的个数为 $ x $，“$\triangle$”的个数为 $ y $，则 $ x $ 与 $ n $ 之间的关系式为x=n+1，$ y $ 与 $ n $ 之间的关系式为y=2n。
(2) 写出 $ y $ 与 $ x $ 之间的关系式：y=2x-2。
(3) 若图 $ n $ 中“$□$”的个数与“$\triangle$”的个数之和为 247，则 $ x = $83。

答案： 14.
(1)x=n+1 y=2n
(2)y=2x-2
(3)83