第66页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 如图,射线$l_{甲}$,$l_{乙}$分别表示甲、乙两名运动员在自行车比赛中所行路程$s(m)$与时间$t(min)$的函数图象,则他们行进的速度关系是(
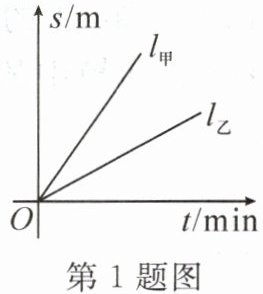
A.甲、乙同速
B.甲比乙快
C.乙比甲快
D.无法确定
B
)
A.甲、乙同速
B.甲比乙快
C.乙比甲快
D.无法确定
答案:
1.B
2. 如图,甲、乙两人以相同路线前往离学校$12km$的地方参加植树活动,图中$l_{甲}$,$l_{乙}$分别表示甲、乙两人前往目的地所行驶的路程$s(km)$与时间$t(min)$的关系. 根据图象判断下列说法错误的是(
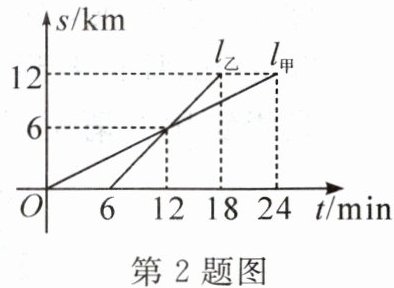
A.甲比乙早出发$6min$
B.甲行驶的路程$s$与时间$t$之间的关系式为$s = 0.5t$
C.甲的速度是$0.5km/min$,乙的速度是$1km/min$
D.乙出发$12min$后两人相遇,这时他们离学校$6km$
D
)
A.甲比乙早出发$6min$
B.甲行驶的路程$s$与时间$t$之间的关系式为$s = 0.5t$
C.甲的速度是$0.5km/min$,乙的速度是$1km/min$
D.乙出发$12min$后两人相遇,这时他们离学校$6km$
答案:
2.D
3. 小明和小亮相约从学校前往博物馆,小明因有事,比小亮晚一些出发. 如图,$y_{1}=k_{1}t$,$y_{2}=k_{2}t + b$分别是小明、小亮行走的路程$y(m)$与小明追赶时间$t(s)$之间的关系图象.
(1) 观察图象可知,小亮比小明先走了
(2) 求$k_{1}$,$k_{2}$的值,并解释$k_{2}$的实际意义.
 ]
]
(1) 观察图象可知,小亮比小明先走了
100
$m$.(2) 求$k_{1}$,$k_{2}$的值,并解释$k_{2}$的实际意义.
 ]
]
答案:
3.解:
(1)100
(2)将点(20,60)代入$y_1 = k_1t$,得$k_1 = 3$.根据题意,得$100 = b$,①$140 = 20k_2 + b$.② 将①代入②,得$k_2 = 2$.$k_2$的实际意义是小亮的速度是2m/s.
(1)100
(2)将点(20,60)代入$y_1 = k_1t$,得$k_1 = 3$.根据题意,得$100 = b$,①$140 = 20k_2 + b$.② 将①代入②,得$k_2 = 2$.$k_2$的实际意义是小亮的速度是2m/s.
4. 李强用甲、乙两种具有恒温功能的热水壶同时加热相同质量的水,甲壶比乙壶加热速度快. 在一段时间内,水温$y(^{\circ}C)$与加热时间$x(s)$之间近似满足一次函数关系,根据记录的数据,画函数图象如图.
(1) 加热前水温是
(2) 求乙壶中水温$y$关于加热时间$x$的关系式.
(3) 当甲壶中水温刚达到$80^{\circ}C$时,乙壶中水温是
 ]
]
(1) 加热前水温是
20℃
.(2) 求乙壶中水温$y$关于加热时间$x$的关系式.
(3) 当甲壶中水温刚达到$80^{\circ}C$时,乙壶中水温是
65℃
. ]
]
答案:
4.解:
(1)20℃
(2)设乙壶中水温$y$关于加热时间$x$的关系式为$y = kx + b$.根据题意,得$20 = b$,①$80 = 160k + b$.② 将①代入②,得$k = \frac {3} {8}$. 乙壶中水温$y$关于加热时间$x$的关系式为$y = \frac {3} {8}x + 20$.
(3)65℃
(1)20℃
(2)设乙壶中水温$y$关于加热时间$x$的关系式为$y = kx + b$.根据题意,得$20 = b$,①$80 = 160k + b$.② 将①代入②,得$k = \frac {3} {8}$. 乙壶中水温$y$关于加热时间$x$的关系式为$y = \frac {3} {8}x + 20$.
(3)65℃
5. 某鲜花销售公司每月付给销售人员的工资有两种方案.
方案一:没有底薪,只付销售提成.
方案二:底薪加销售提成.
下图中的射线$l_{1}$、射线$l_{2}$分别表示该鲜花销售公司每月按方案一、方案二付给销售人员的工资$y_{1}$(元)和$y_{2}$(元)与其当月鲜花销售量$x$(千克)$(x\geq0)$的函数关系.
(1) 分别求$y_{1}$,$y_{2}$与$x$之间的函数表达式.
(2) 若该公司某销售人员今年$3$月份的鲜花销售量没有超过$70$千克,但其$3$月份的工资超过$2000$元,则该公司采用了方案
 ]
]
方案一:没有底薪,只付销售提成.
方案二:底薪加销售提成.
下图中的射线$l_{1}$、射线$l_{2}$分别表示该鲜花销售公司每月按方案一、方案二付给销售人员的工资$y_{1}$(元)和$y_{2}$(元)与其当月鲜花销售量$x$(千克)$(x\geq0)$的函数关系.
(1) 分别求$y_{1}$,$y_{2}$与$x$之间的函数表达式.
(2) 若该公司某销售人员今年$3$月份的鲜花销售量没有超过$70$千克,但其$3$月份的工资超过$2000$元,则该公司采用了方案
一
给这名销售人员付$3$月份的工资. ]
]
答案:
5.解:
(1)设$y_1 = k_1x$.根据题意,得$40k_1 = 1200$,解得$k_1 = 30$. $\therefore y_1 = 30x(x \geq 0)$.设$y_2 = k_2x + b$.根据题意,得$800 = b$,①$1200 = 40k_2 + b$.②将①代入②,得$k_2 = 10$.$\therefore y_2 = 10x + 800(x \geq 0)$.
(2)一
(1)设$y_1 = k_1x$.根据题意,得$40k_1 = 1200$,解得$k_1 = 30$. $\therefore y_1 = 30x(x \geq 0)$.设$y_2 = k_2x + b$.根据题意,得$800 = b$,①$1200 = 40k_2 + b$.②将①代入②,得$k_2 = 10$.$\therefore y_2 = 10x + 800(x \geq 0)$.
(2)一
查看更多完整答案,请扫码查看


