《2025年名校课堂八年级数学上册北师大版内蒙古专版》

1. 新考向 数学文化 公元前 6 世纪，古希腊的毕达哥拉斯学派有一种观点——“万物皆数”，即一切量都可以用整数或整数的比(分数)表示。后来这一学派中的希帕索斯发现，边长为 1 的正方形对角线的长度不能用整数或整数的比表示，这令毕达哥拉斯学派感到惊恐不安，由此引发了第一次数学危机。这类“不能用整数或整数的比表示的数”指的是(B)

A.有理数
B.无理数
C.零
D.负数

答案： 1.B

2. (教材 P25“尝试·思考”变式)两直角边长分别为 2 和 3 的直角三角形的斜边长是(D)

A.整数
B.分数
C.有理数
D.无理数

答案： 2.D

3. (2024·泸州)下列各数中，是无理数的是(D)

A.$-\dfrac{1}{3}$
B.3.14
C.0
D.$\pi$

答案： 3.D

4. 下列说法中，正确的是(D)

A.有理数是有限小数
B.无理数可以写成分数的形式
C.无理数是无限循环小数
D.无限不循环小数是无理数

答案： 4.D

5. （教材 P27 例变式）把下列各数填入对应的集合内：
$2,\dfrac{1}{3},0.1212212221\cdots$（相邻两个 1 之间 2 的个数逐次加 1），$2.\dot{0}\dot{2},3\pi,3.14,0,-\dfrac{23}{5}$。
有理数集合：$\{\cdots\}$。
无理数集合：$\{\cdots\}$。

答案： $5.2,\frac{1}{3},2.02,3.14,0,-\frac{23}{5},0.1212212221\cdots（$相邻两个1之间2的个数逐次加1），$3\pi$

6. 实数的分类：

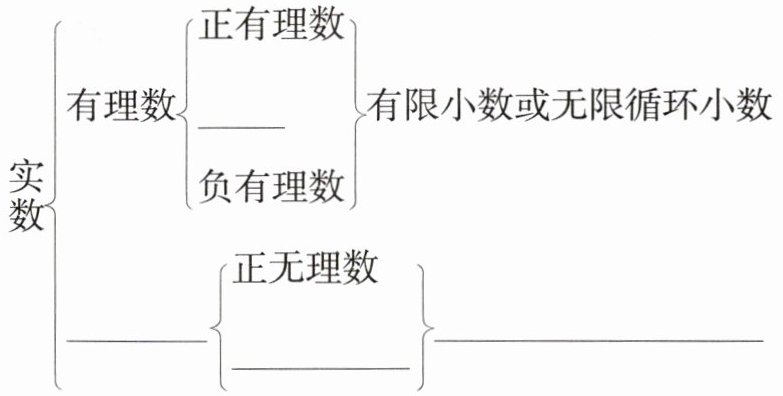
答案： 6.0 无理数 负无理数 无限不循环小数

7. 下列说法中，正确的是(C)

A.无理数包括正无理数、零和负无理数
B.无限小数都是无理数
C.正实数包括正有理数和正无理数
D.实数可以分为正实数和负实数两类

答案： 7.C

8. 把下列各数分别填入相应的集合内。
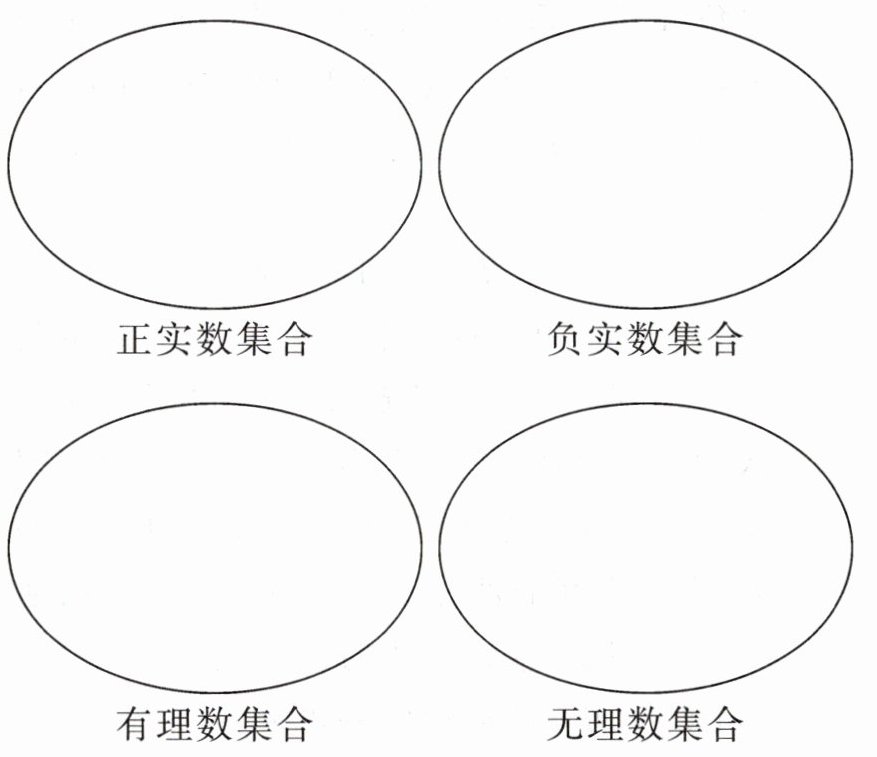
$\dfrac{1}{2},0,3.00\dot{1},-\dfrac{11}{12},-5.21212121\cdots$（相邻两个 2 之间有 1 个 1），$\dfrac{3}{2}\pi,6.1234567\cdots$（小数部分由相继的正整数组成），$(\pi - 3.14)^0,-0.303003003,-215$。

答案： 正实数集合：$\dfrac{1}{2},3.00\dot{1},\dfrac{3}{2}\pi,6.1234567\cdots$（小数部分由相继的正整数组成）$,(\pi - 3.14)^0$
负实数集合：$-\dfrac{11}{12},-5.21212121\cdots$（相邻两个 2 之间有 1 个 1）$, -0.303003003,-215$
有理数集合：$\dfrac{1}{2},0,3.00\dot{1},-\dfrac{11}{12},-5.21212121\cdots$（相邻两个 2 之间有 1 个 1）$,(\pi - 3.14)^0,-0.303003003,-215$
无理数集合：$\dfrac{3}{2}\pi,6.1234567\cdots$（小数部分由相继的正整数组成）