第3页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
10. 在Rt△ABC中,斜边$BC = 10$,则$BC^{2}+AB^{2}+AC^{2}=$(
A.20
B.100
C.200
D.144
C
)A.20
B.100
C.200
D.144
答案:
10.C
11. 如图,在Rt△ABC中,若$\angle C = 90^{\circ}$,$AC = 3$,$BC = 4$,则点C到直线AB的距离为(
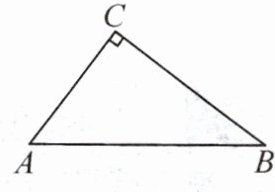
A.3
B.4
C.5
D.2.4
D
)
A.3
B.4
C.5
D.2.4
答案:
11.D
12. (教材P9习题T6变式)已知等腰三角形的腰长为5cm,底边上的中线长为4cm,则它的面积是(
A.$24$ $cm^{2}$
B.$20$ $cm^{2}$
C.$15$ $cm^{2}$
D.$12$ $cm^{2}$
D
)A.$24$ $cm^{2}$
B.$20$ $cm^{2}$
C.$15$ $cm^{2}$
D.$12$ $cm^{2}$
答案:
12.D
13. 如图所示的是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形.若正方形A,B,C,D的面积分别是4,6,2,4,则最大正方形E的面积是(
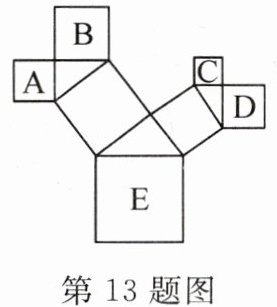
A.12
B.14
C.16
D.18
C
)
A.12
B.14
C.16
D.18
答案:
13.C
14. 如图,在边长为1的小正方形网格中,P为CD上任意一点,则$PB^{2}-PA^{2}$的值为
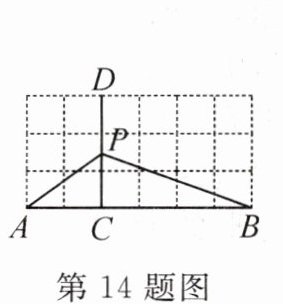
12
.
答案:
14.12
15. 如图,在四边形草坪ABCD中,$\angle B=\angle D = 90^{\circ}$.若$AB = 20$m,$BC = 15$m,$CD = 7$m,求这块草坪ABCD的面积.
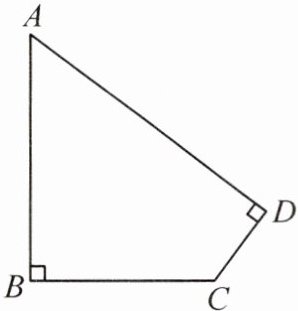

答案:
15.解:连接AC.在Rt△ABC中,由勾股定理,得$AC^{2}=AB^{2}+BC^{2}=20^{2}+15^{2}=625=25^{2}$.
∴AC=25m.在Rt△ADC中,由勾股定理,得$AD^{2}+CD^{2}=AC^{2}$,
∴$AD^{2}=AC^{2}-CD^{2}=24^{2}$.
∴AD=24m.
∴$S_{四边形ABCD}=\frac{1}{2}AB·BC+\frac{1}{2}AD·CD=\frac{1}{2}×20×15+\frac{1}{2}×24×7=234(m^{2})$.
∴这块草坪ABCD的面积为234$m^{2}$.
∴AC=25m.在Rt△ADC中,由勾股定理,得$AD^{2}+CD^{2}=AC^{2}$,
∴$AD^{2}=AC^{2}-CD^{2}=24^{2}$.
∴AD=24m.
∴$S_{四边形ABCD}=\frac{1}{2}AB·BC+\frac{1}{2}AD·CD=\frac{1}{2}×20×15+\frac{1}{2}×24×7=234(m^{2})$.
∴这块草坪ABCD的面积为234$m^{2}$.
16. 人大附中校本经典题根据勾股定理知识迁移,解答下列问题.
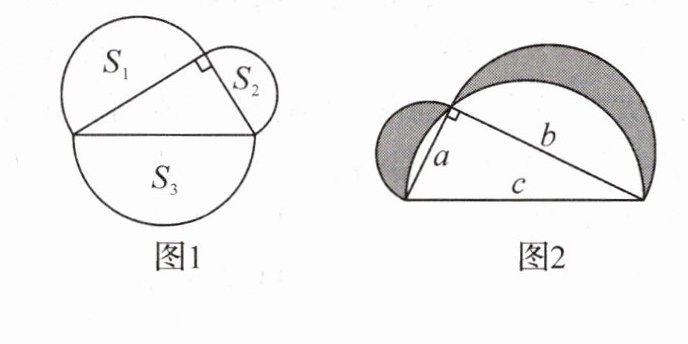
(1)如图1,分别以直角三角形的三边为直径向外侧作半圆,求它们的面积$S_{1}$,$S_{2}$,$S_{3}$之间满足的等量关系.
(2)应用:如图2,直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为直径作半圆.若$a = 3$,$c = 5$,求图中阴影部分的面积.
(1)如图1,分别以直角三角形的三边为直径向外侧作半圆,求它们的面积$S_{1}$,$S_{2}$,$S_{3}$之间满足的等量关系.
(2)应用:如图2,直角三角形的两条直角边长分别为a,b,斜边长为c,分别以三边为直径作半圆.若$a = 3$,$c = 5$,求图中阴影部分的面积.

答案:
16.解:
(1)设$S_{1}$,$S_{2}$,$S_{3}$分别对应直径为a,b,c,根据勾股定理,得$a^{2}+b^{2}=c^{2}$.由图,得$S_{1}=\frac{1}{2}\pi(\frac{a}{2})^{2}=\frac{\pi}{8}a^{2}$,同理可得,$S_{2}=\frac{\pi}{8}b^{2}$,$S_{3}=\frac{\pi}{8}c^{2}$,
∴$S_{1}+S_{2}=\frac{\pi}{8}a^{2}+\frac{\pi}{8}b^{2}=\frac{\pi}{8}(a^{2}+b^{2})=\frac{\pi}{8}c^{2}=S_{3}$.
(2)设以a,b,c为直径的三个半圆的面积分别为P,Q,R,以a,b为直角边的直角三角形的面积为$S_{4}$.
∵a=3,c=5,
∴$b^{2}=c^{2}-a^{2}=5^{2}-3^{2}=16=4^{2}$.
∴b=4.
∴$S_{4}=\frac{1}{2}ab=\frac{1}{2}×3×4=6$.由
(1)知,P+Q=R,
∴阴影部分的面积为S=P+Q+$S_{4}$-R=$S_{4}$=6.
(1)设$S_{1}$,$S_{2}$,$S_{3}$分别对应直径为a,b,c,根据勾股定理,得$a^{2}+b^{2}=c^{2}$.由图,得$S_{1}=\frac{1}{2}\pi(\frac{a}{2})^{2}=\frac{\pi}{8}a^{2}$,同理可得,$S_{2}=\frac{\pi}{8}b^{2}$,$S_{3}=\frac{\pi}{8}c^{2}$,
∴$S_{1}+S_{2}=\frac{\pi}{8}a^{2}+\frac{\pi}{8}b^{2}=\frac{\pi}{8}(a^{2}+b^{2})=\frac{\pi}{8}c^{2}=S_{3}$.
(2)设以a,b,c为直径的三个半圆的面积分别为P,Q,R,以a,b为直角边的直角三角形的面积为$S_{4}$.
∵a=3,c=5,
∴$b^{2}=c^{2}-a^{2}=5^{2}-3^{2}=16=4^{2}$.
∴b=4.
∴$S_{4}=\frac{1}{2}ab=\frac{1}{2}×3×4=6$.由
(1)知,P+Q=R,
∴阴影部分的面积为S=P+Q+$S_{4}$-R=$S_{4}$=6.
查看更多完整答案,请扫码查看


