第14页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 小明用火柴棒摆直角三角形,已知他摆两条直角边分别用了 6 根和 8 根火柴棒,则他摆完这个直角三角形共用火柴棒(
A.20 根
B.14 根
C.24 根
D.30 根
C
)A.20 根
B.14 根
C.24 根
D.30 根
答案:
1.C
2. (2023·银川期中)如图,在 $ Rt \triangle ABC $ 中, $ \angle ACB = 90^{\circ} $, $ CD $ 是高, $ AC = 4 cm $, $ BC = 3 cm $,则 $ CD = $(
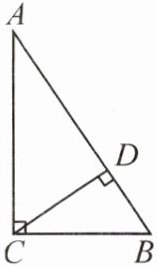
A.$ 5 cm $
B.$ \dfrac{12}{5} cm $
C.$ \dfrac{5}{12} cm $
D.$ \dfrac{4}{3} cm $
B
)
A.$ 5 cm $
B.$ \dfrac{12}{5} cm $
C.$ \dfrac{5}{12} cm $
D.$ \dfrac{4}{3} cm $
答案:
2.B
3. 在学习勾股定理时,甲同学用四个相同的直角三角形(直角边长分别为 $ a,b $,斜边长为 $ c $)构成如图所示的正方形;乙同学用边长分别为 $ a,b $ 的两个正方形和长为 $ b $,宽为 $ a $ 的两个长方形构成如图所示的正方形. 甲、乙两位同学给出的构图方案中,可以证明勾股定理的是(
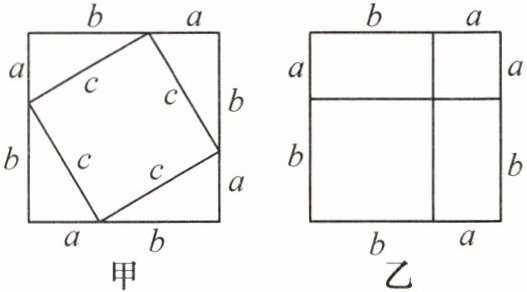
A.甲
B.乙
C.甲、乙都可以
D.甲、乙都不可以
A
)
A.甲
B.乙
C.甲、乙都可以
D.甲、乙都不可以
答案:
3.A
4. 如图, $ \angle OAB = \angle OBC = \angle OCD = 90^{\circ} $, $ AB = BC = CD = 1 $, $ OA = 2 $,则 $ OD^{2} = $
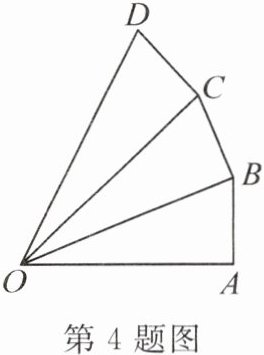
7
.
答案:
4.7
5. 如图,在 $ Rt \triangle ABC $ 中, $ \angle ACB = 90^{\circ} $, $ AB = 4 cm $,以 $ Rt \triangle ABC $ 的三边为直角边分别向外作等腰直角三角形,则图中阴影部分的面积为
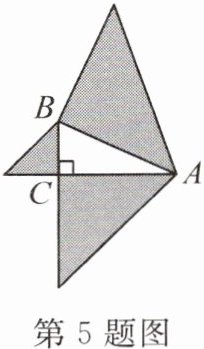
16 cm²
.
答案:
5.16 cm²
6. 如图,在 $ \triangle ABC $ 中, $ \angle C = 90^{\circ} $, $ M $ 是 $ BC $ 的中点, $ MD \perp AB $ 于点 $ D $,试说明: $ AD^{2} = AC^{2} + BD^{2} $.
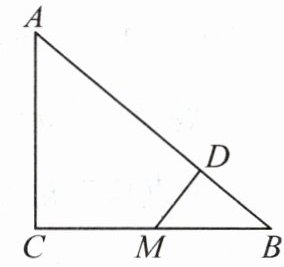

答案:
6.解:连接MA.MD⊥AB,
∴∠ADM=∠BDM=90°.
∴AD² = AM² - MD²,MD² = BM² - BD².
∵∠C = 90°,
∴AM² = AC² + MC².
∵M为BC的中点,
∴BM = MC.AD² = AM² - MD² = AM² - BM² + BD² = AM² - MC² + BD² = AC² + BD².
∴∠ADM=∠BDM=90°.
∴AD² = AM² - MD²,MD² = BM² - BD².
∵∠C = 90°,
∴AM² = AC² + MC².
∵M为BC的中点,
∴BM = MC.AD² = AM² - MD² = AM² - BM² + BD² = AM² - MC² + BD² = AC² + BD².
7. 如图,正方形网格中是直角三角形的是(
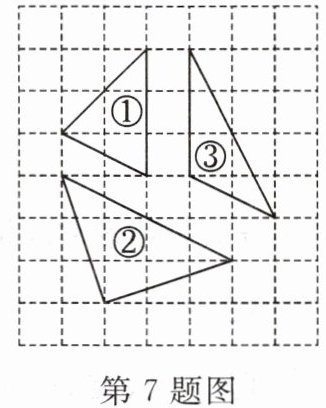
A.①
B.②
C.③
D.①②
B
)
A.①
B.②
C.③
D.①②
答案:
7.B
8. 新考向 开放性问题 将勾股数 $ 3,4,5 $ 扩大到原来的 2 倍、3 倍、4 倍……可以得到勾股数 $ 6,8,10 $; $ 9,12,15 $; $ 12,16,20 $;…,则我们把 $ 3,4,5 $ 这样的勾股数称为基本勾股数,请你写出两组不同于以上所给出的基本勾股数:
答案不唯一,如:5,12,13;7,24,25
.
答案:
8.答案不唯一,如:5,12,13;7,24,25
9. 如图, $ \angle BAC = 90^{\circ} $, $ AB = 4 $, $ AC = 4 $, $ BD = 7 $, $ DC = 9 $,则 $ \angle DBA = $
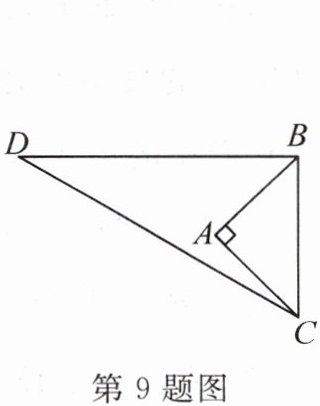
45°
.
答案:
9.45°
查看更多完整答案,请扫码查看


